El Árbol de Segmentos / Segment Tree es una estructura de datos que sirve para gestionar de forma eficiente consultas de información y actualizaciones sobre intervalos de un array. Un ejemplo es el problema de Range Minimum Query, es decir, consultar el mínimo valor del array en un intervalo. La idea básica es la siguiente: se forma un árbol binario donde cada nodo contiene el resultado de aplicar la operación que queremos sobre un intervalo (segmento), la raíz es el intervalo completo y los dos hijos de cada nodo son los nodos correspondientes a los dos subintervalos correspondientes a dividir el intervalo del padre por la mitad. Con esta estructura construida, sólo es necesario visitar $\mathcal{O}(\log n)$ nodos para obtener el resultado correspondiente a un intervalo cualquiera. Veamos un ejemplo.
Consideremos el siguiente array:
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| a[i] | 5 | 1 | 4 | 6 | 7 | 3 | 8 | 2 |
El correspondiente árbol de segmentos es este.
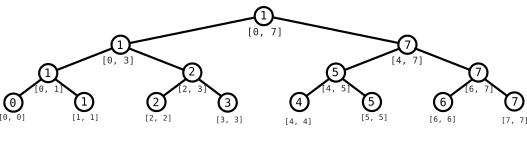
Aquí en cada nodo hemos escrito el índice de la array que tiene el valor mínimo para el intervalo correspondiente, no el valor mínimo en sí. Por ejemplo, se puede ver que el valor mínimo global de la array se toma en el índice $1$, y por eso el $1$ es el valor de la raíz, pero en los intervalos $[4, 7]$, $[6, 7]$ y $[7, 7]$ el valor mínimo ($2$) se toma en el índice $7$, y por eso los nodos correspondientes a esos intervalos tienen ese valor. Podríamos haberlo hecho con el valor mínimo (y así igual se vería más claramente cómo está construido el árbol: en cada nodo está el valor menor de sus dos hijos), pero lo hemos hecho con el índice porque tener el índice siempre es estrictamente mejor que tener el valor: mientras que teniendo el índice se puede obtener inmediatamente el valor, al revés no es así, y es usual que en un problema no te pidan el valor mínimo de la array en sí sino una información asociada a la posición donde se alcanza el mínimo.
El árbol se construye recursivamente: a partir de los valores de los nodos hijos se determina el valor del nodo padre a partir de en qué índice se toma un valor menor. Veremos más detalles de cómo implementar la construcción del árbol en el siguiente manual: aquí sólo explicaremos el funcionamiento abstracto.
Para ver cómo funciona un árbol de segmentos, seguiremos paso por paso qué ocurre en la consulta del mínimo valor en el intervalo $[2, 6]$ para el árbol de segmentos anterior.
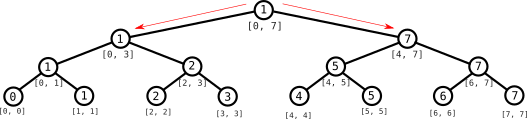
Empezamos en la raíz del árbol. El intervalo correspondiente a esa raíz, el $[0, 7]$, es más grande que el intervalo que hemos pedido, así que no podemos utilizar directamente la información de ese nodo: necesitamos consultar información de los subárboles izquierdo y derecho. Lo que haremos será consultar en cada subárbol el valor mínimo que se toma dentro de la intersección del intervalo $[2, 6]$ y los subintervalos correspondientes a los dos subárboles, es decir, del subárbol izquierdo obtendremos el mínimo en el intervalo $[2, 3]$ y del subárbol derecho obtendremos el mínimo del intervalo $[4, 6]$: comparando los dos valores obtendremos el mínimo en el intervalo completo. Empecemos por el subárbol izquierdo.
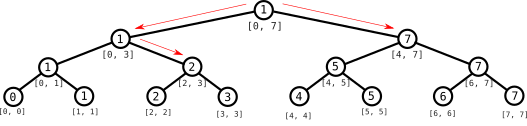
Ahora estamos en el nodo $[0, 3]$. Nuestro objetivo es reportar el índice donde se toma el valor mínimo de la intersección de $[2, 6]$ con $[0, 3]$: igual que antes, no podemos usar el valor que está guardado en el nodo, porque ese valor tiene en cuenta los elementos con índices $0$ y $1$, que están fuera del intervalo deseado. Esta vez, sin embargo, sólo es relevante el subárbol derecho, porque el intervalo $[0, 1]$ no nos importa.
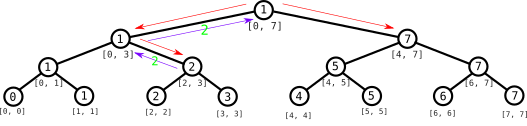
Cuando llegamos al nodo del intervalo $[2, 3]$, ya podemos aprovechar la información del nodo: dado que $[2, 3]$ está incluido en $[2, 6]$, no hay ningún elemento que esté fuera y podemos retornar directamente el índice que está en el nodo. (Decimos “retornar” porque la implementación más común es a través de funciones recursivas). Desde el nodo $[0, 3]$ retornamos el índice que hemos recibido. Ahora estamos de vuelta en la raíz: exploremos el subárbol derecho.
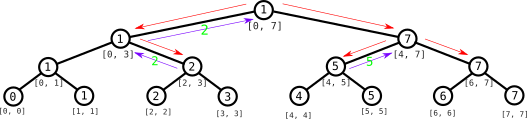
Cuando descendemos al nodo correspondiente a $[4, 7]$, ahora tenemos que volver a explorar los dos subárboles otra vez, porque nuestro intervalo es demasiado grande, pero en ambos intervalos hay elementos que nos interesan. Como antes, cuando vamos al nodo $[4, 5]$ devolvemos directamente el valor que está en el nodo, ya que $[4, 5]$ está contenido en $[2, 6]$.
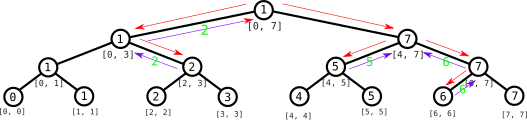
Cuando vamos al nodo con $[6, 7]$ ahora sólo nos interesa el subárbol izquierdo. Retornamos el índice 6 del nodo $[6, 6]$ y lo volvemos a retornar en el nodo $[6, 7]$, subiendo hasta el nodo $[4, 7]$: ahora en este nodo hemos recibido dos índices de los dos subárboles correspondientes y tenemos que devolver el que tiene menor valor de los dos, que es $5$ porque $a_5 = 3 < 8 = a_6$.
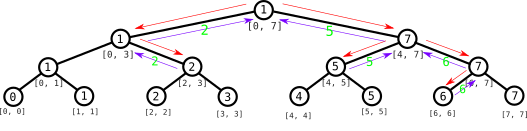
En la raíz procedemos igualmente: como $a_5 = 3 < 4 = a_2$, el índice que buscamos es 5.
En general, el funcionamiento de un árbol de segmentos para RMQ sigue el siguiente esquema recursivo:
RMQ(NODO, INTERVALO):
-Si el intervalo correspondiente a NODO está contenido dentro de INTERVALO, retorna índice almacenado en NODO.
-Si no, llama a RMQ(NODO->HIJO IZQUIERDO, INTERVALO) o RMQ(NODO->HIJO DERECHO, INTERVALO) o a ambos y retorna el índice que recibe (si llama a los dos, retorna el de menor valor).
Puede no resultar inmediatamente obvio que esta recursividad tiene complejidad $\mathcal{O}(\log n)$, ya que en algunos casos se visitan los dos subárboles por cada nodo. Para demostrarlo, vemos que se cumple la siguiente propiedad: después de la primera vez que se tienen que visitar los dos subárboles, la intersección del intervalo de consulta con los intervalos de los nodos contiene algún extremo de los intervalos de los nodos, es decir, no ocurre que el intervalo de consulta esté estrictamente dentro del intervalo de un nodo. Por ejemplo, en el caso anterior en la raíz el intervalo de consulta $[2, 6]$ no contiene ninguno de los extremos del intervalo $[0, 7]$, pero después tanto $[0, 3]$ como $[4, 7]$ tienen alguno de sus extremos dentro de $[2, 6]$.
Una vez ocurre esto, vemos que realmente no puede haber una bifurcación “significativa” porque, aunque es posible que se vuelva a tener que consultar los dos nodos hijos, uno de los hijos estará contenido dentro del intervalo a consultar y retornará el valor inmediatamente. (Esto ocurre en el ejemplo anterior cuando se visita el nodo $[4, 7]$: como $[2, 6]$ contiene $[4, 5]$, la consulta al subárbol izquierdo es sólo una consulta al nodo hijo izquierdo) Por tanto, se hacen como máximo dos descensos hasta las hojas del árbol, visitando como mucho $2$ nodos por cada nivel en cada descenso, para visitar como máximo $4\log(2n) = \mathcal{O}(\log n)$ nodos.


Añadir nuevo comentario