En el manual anterior vimos cómo hacer calcular actualizaciones de un sólo valor en un árbol de segmentos en $\mathcal{O}(\log n)$. Aquí veremos una técnica, denominada lazy propagation, que permite hacer actualizaciones en intervalos en $\mathcal{O}(\log n)$ por actualización.
Por supuesto, actualizar todas las posiciones del vector correspondiente tiene un coste proporcional a la longitud del intervalo, por lo que para este problema no vamos a trabajar con el vector, sino que sólo utilizaremos el árbol de segmentos. La idea importante de la técnica lazy propagation es que no es necesario actualizar el valor de todos los nodos que cambien de golpe, sino que los vamos actualizando conforme los vamos necesitando. Ilustraremos la técnica con un ejemplo concreto.
Tenemos el siguiente problema: queremos una estructura de datos que permita calcular RSQ (suma de elementos en un intervalo) en un vector que puede recibir actualizaciones del siguiente tipo: para $i$, $j$, $v$, todos los valores en el intervalo $[i, j]$ pasan a ser $v$. Vamos a ver cómo lo haríamos sobre este vector en concreto:
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| a[i] | 5 | 1 | 4 | 7 | 6 | 3 | 8 | 2 |
El árbol de segmentos de RSQ para este vector es el siguiente:
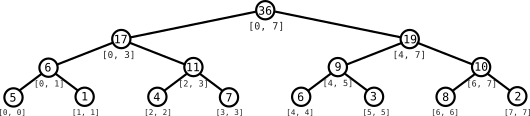
Supongamos que tenemos una actualización que iguala todos los elementos en el intervalo $[0, 5]$ a $10$. Vamos descendiendo por el árbol como lo haríamos para responder a una consulta hasta llegar a los nodos en los que se particiona el intervalo, en este caso $[0, 3]$ y $[4, 5]$. Podemos actualizar los valores de estos nodos: como sabemos que con esta actualización los valores de todos los elementos en su intervalo correspondiente van a ser iguales a $10$, el valor de la suma del intervalo es igual a $10$ multiplicado por la longitud del intervalo, que resulta en $40$ y $20$, respectivamente. Pero actualizar estos dos nodos no es suficiente, porque los nodos que hay por debajo siguen teniendo el valor anterior y si hiciéramos una consulta de los intervalos correspondientes a estos nodos obtendríamos un valor incorrecto. Sin embargo, si actualizamos todos los nodos el coste acabaría siendo proporicional a la longitud del intervalo, que es algo que no queremos. La solución es dejar un “aviso” en los hijos de cada nodo de que el subárbol tiene que ser actualizado con el valor $10$. Así, cuando lo necesitemos calcularemos los valores necesarios.
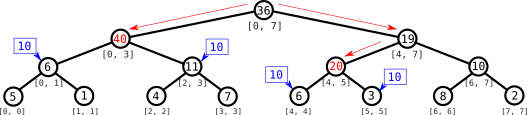
Ahora actualizamos todos los nodos por los que hemos pasado durante el descenso, ya que los valores de estos habrán cambiado tras la actualización (sólo hace falta volver a sumar los valores de los dos hijos). Nótese que todo esto lo hacemos en $\mathcal{O}(\log n)$, ya que el descenso se hace igual que en una consulta y ya vimos que la cantidad de nodos que se visitaba era logarítmica.
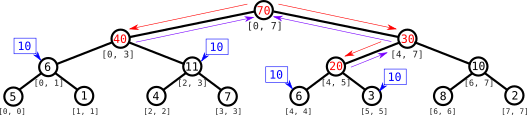
Veamos ahora cómo vamos a usar estos “avisos”. Hagamos una consulta de la suma del intervalo $[1, 3]$. Descendemos hasta el nodo del intervalo $[0, 1]$ y encontramos que tiene un aviso: tenemos que actualizar su valor (aunque en esta consulta no lo necesitemos: nos conviene hacer las actualizaciones cuando se visita el nodo). Actualizamos su valor a $20$ y “propagamos” el aviso: ahora dejamos aviso de que tenemos que actualizar sus dos hijos.
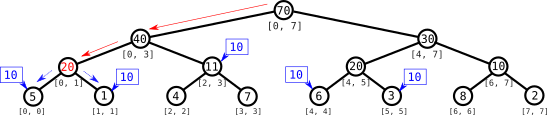
El valor que es relevante para nuestro intervalo es el del intervalo $[1, 1]$, así que descendemos al nodo de ese intervalo y, al ver que tiene un aviso, actualizamos su valor a $10$. Como no tiene hijos, esta vez no propagamos el aviso. Nótese que no visitamos el nodo $[0, 0]$ en esta consulta y por tanto no es necesario que actualicemos su valor.
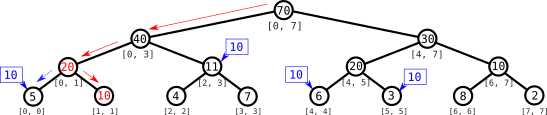
Devolvemos el valor $10$ y subimos por el árbol. El siguiente nodo que nos interesa es el del intervalo $[2, 3]$.
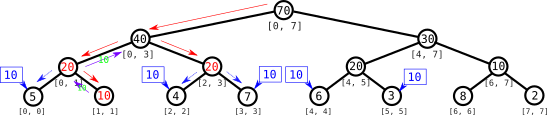
Al ver que tiene un aviso, actualizamos su valor a $20$ y propagamos el aviso a sus dos hijos. No tenemos que descender más para esta consulta, así que retornamos el valor $20$ y finalmente obtenemos que la suma deseada es $30$.
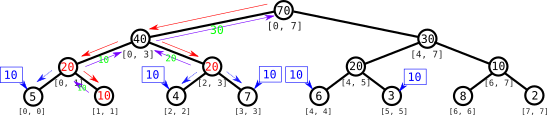
La idea principal de la técnica de lazy propagation es esta que hemos visto: dejar “avisos” (flags) de actualizaciones pendientes que realizamos cuando visitamos el nodo, aprovechando el descenso que vamos haciendo por el árbol para ir “propagando” estos avisos a los hijos y sólo actualizar los nodos que visitamos. Comprobar que hay un aviso, actualizar la información y propagar el aviso solo cuesta $\mathcal{O}(1)$ de tiempo por cada visita, así que la complejidad asintótica temporal es la misma. Dicho de otro modo, como en cada consulta visitamos $\mathcal{O}(\log n)$ nodos, el número de actualizaciones y propagaciones es $\mathcal{O}(\log n)$ también.
Podemos preguntarnos qué pasa si propagamos un aviso a un nodo que ya tiene un aviso. En el problema que hemos planteado, el aviso se sobreescribe, pero en otros casos puede no ser así. Por ejemplo, si en lugar de asignar un valor a un intervalo tuviéramos que sumar un valor a todos los elementos de un intervalo, entonces al propagar un aviso a un nodo que ya tiene aviso se tendrían que sumar los valores de los avisos. Hay problemas en los que la cuestión de cómo se tienen que combinar varias actualizaciones es una consideración importante.
Implementar la lazy propagation con la implementación del árbol de segmentos que vimos en el manual anterior no es muy complicado: hay que añadir un par de vectores adicionales que almacenen por cada nodo si hay un aviso y el valor del aviso y llamar a una función que haga la actualización y propagación siempre que visitemos un nodo.


Añadir nuevo comentario