Una de las técnicas más sencillas para resolver un problema computacionalmente es generar todos los posibles candidatos a ser solución y después comprobar cuáles comportan una solución válida. Para ilustrar el concepto, presentamos un problema clásico:
Ejemplo: N reinas
En un tablero de Ajedrez $N \times N$, queremos colocar $N$ reinas tal que no se amenacen entre ellas (es decir, que no haya dos que estén en la misma fila, columna o diagonal). ¿Cuántas maneras hay de hacer esto?
Una posible solución a este problema, siguiendo la filosofía del primer párrafo es generar las todas las posiciones posibles de las $N$ reinas en el tablero $N \times N$ y para cada una de ellas comprobar si es una posición válida o no. Veamos cómo se implementaría esta solución:
int N;
vector<int> reinas;
int sol = 0;
bool amenaza(int a, int b) {
int x1 = a % N;
int x2 = b % N;
int y1 = a / N;
int y2 = b / N;
return (x1 == x2 or y1 == y2 or x1+y1 == x2+y2 or x1-y1 == x2-y2);
}
bool posicion_correcta() {
for (int i = 0; i < N; ++i) {
for (int j = i+1; j < N; ++j) {
if (amenaza(reinas[i], reinas[j])) return false;
}
}
return true;
}
void backtracking_reinas(int i) {
if (i == N) {
if (posicion_correcta()) ++sol;
return;
}
int primera_posicion = 0;
if (i > 0) primera_posicion = reinas[i-1]+1;
for (int pos = primera_posicion; pos < N*N; ++pos) {
reinas[i] = pos;
backtracking_reinas(i+1);
}
}
Analicemos el código. La función amenaza retorna si dadas dos posiciones de reinas en un tablero se amenazan entre sí. La función posicion_correcta retorna si no hay ningún par de reinas que se amenacen entre ellas (para las posiciones que tenemos guardados en el vector reinas). Estas dos funciones son llamadas por la función que es realmente interesante: backtracking_reinas. Esta función irá rellenando el vector reinas, generando todas las posibles posiciones. Su parámetro i es el número de reina que actualmente estamos colocando (se entenderá mejor en la explicación del código)
Expliquemos ahora cómo funciona el código: la primera llamada a la función backtracking_reinas se realiza con i=0. No se cumple la condición para ninguno de los ifs, así que los ignoramos por ahora. Lo que hace esa función en su primera llamada es entrar en un bucle para una variable pos desde 0 hasta N^2-1, en la que en cada iteración asigna la posición pos a la primera reina (0-ésima, empezando desde 0) y llama a la función backtracking_reinas, esta vez con i=1. En cada una de estas llamadas, vuelve a entrar en el bucle, pero esta vez no empezando desde la posición 0, sino desde la posición siguiente a la de la reina anterior. Estas llamadas recursivas se repiten hasta que llegamos a i = N, cuando ya hemos colocado todas las reinas, en las que la función ya no entra en el bucle sino que comprueba si la posición actual de las reinas es una solución válida.
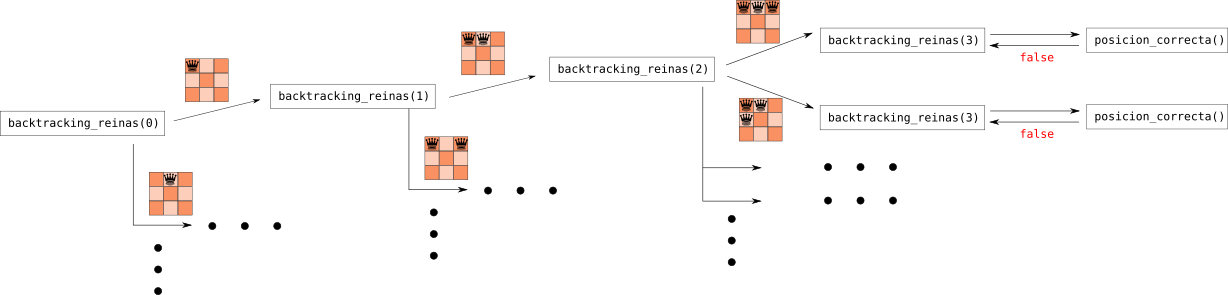
Ilustración de la ejecución del programa para el caso N = 3.
Figura de la reina proveniente de: https://commons.wikimedia.org/wiki/File:Chess_qdt45.svg , por Colin M. L. Burnett. Licenciada bajo CC-BY-SA.
Debido a cómo funciona la recursividad, después de comprobar por primera vez si las posiciones son váidas, el programa vuelve a la llamada de backtracking_reinas anterior para realizar la siguiente iteración del bucle y colocar la última reina en la siguiente posición: después de comprobar otra vez, la coloca en la siguiente, y en la siguiente… y después de colocar la última reina en todas las posiciones posibles con las N-1 reinas fijas, vuelve a la llamada backtracking_reinas(N-2) para colocar la penúltima reina en la siguiente posición y vuelve a llamar a backtracking_reinas(N-1) para comprobar todas las posiciones posibles de la última reina para esta nueva configuración. Este esquema recursivo recorre todas las opciones posibles.
Generar todas las configuraciones posibles y comprobar cuáles son válidas es la idea básica de la Búsqueda Completa, llamada así porque se busca en todo el espacio de soluciones. Sin embargo, no suele ser muy práctico porque el número de posibilidades puede ser muy grande: en este caso, si hacemos los cálculos para un tablero de ajedrez estándar (N = 8) el número de posiciones es $4426165368$. Teniendo en cuenta que para cada posición tenemos que comprobar que cada par de reinas no se amenace, este algoritmo no terminaría en un tiempo razonable.
Por suerte, podemos hacer ciertas observaciones para reducir mucho el número de posibilidades. En primer lugar, no tiene sentido poner a dos reinas en la misma fila. Si hacemos que la i-ésima reina vaya en la i-ésima fila, el número de posibilidades se reduce a $8^8 = 16777216$. Y si además nos vamos guardando en qué columnas hemos puesto ya una reina para no repetir columna, el número de posibilidades es $8! = 40320$, un número ya muy alcanzable.
Aún se puede mejorar más la eficiencia si además comprobamos que no repetimos diagonal en las posiciones que vamos generando, de forma que ya no haga falta comprobar al final si la posición es correcta o no, ya que todas las posibilidades que llegan hasta el final son correctas. Esto requiere emplear más tiempo durante la generación, pero resulta rentable debido a que se eliminan posibilidades que, siendo incorrectas desde el principio, generan muchas posiciones no válidas que comprobar inútilmente. Esta idea de ir eliminando configuraciones que se ve que no van a dar lugar a una solución válida se llama backtracking, porque se “vuelve atrás” en el árbol de recursividad cuando se rechaza una configuración.
Las ideas importantes de este ejemplo son: el método de ir generando todas las opciones posibles de forma recursiva y que, si el número de posibilidades es demasiado grande, a veces se pueden aprovechar propiedades del problema para reducir el espacio de búsqueda.


Añadir nuevo comentario