Centroid Decomposition es otro tipo de descomposición de árboles que es de gran utilidad para responder a preguntas generales sobre nuestro grafo, especialmente aquellas dirigidas a los caminos del árbol, como por ejemplo:
- ¿Cuántos caminos hay de longitud $k$?
- En un árbol con pesos en las aristas, ¿cuál es el peso mínimo de entre los caminos de longitud $k$? Donde el peso de un camino es la suma de los pesos de las aristas que lo componen.
- En un árbol con pesos en las aristas, ¿cuántos caminos hay tal que el xor de los pesos de sus aristas sea $k$?
El esquema general que siguen los algoritmos que utilizan Centroid Decomposition es:
- Encontrar el centroide (Centroid)
- Solucionar la parte del problema que considera los caminos que pasan por el centroide
- Quitar el centroide del árbol y solucionar el problema para cada uno de los árboles resultantes (utilizando Centroid Decomposition en cada uno de ellos)
- Juntar las soluciones parciales para encontrar el resultado
Qué es el centroide y cómo encontrarlo
El centroide es un nodo que cumple la propiedad de que, si consideramos el árbol arraigado en este nodo, todos los subárboles tienen tamaño menor o igual que la mitad del tamaño del árbol original.
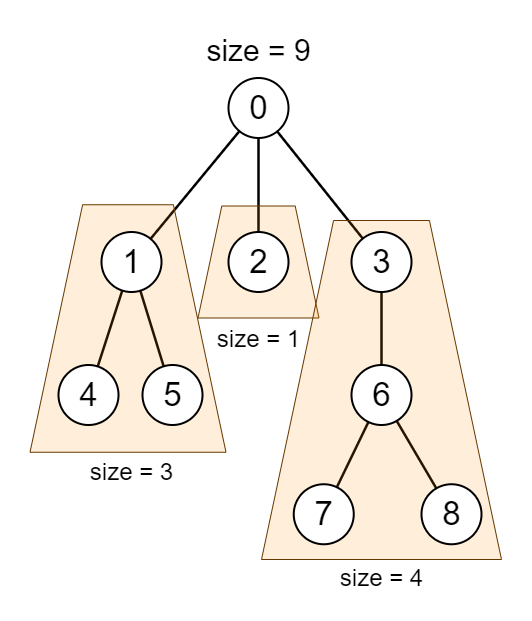
Normalmente, solo hay un centroide en un árbol, pero si hay un número par de nodos, podría haber dos, que serían vecinos.
Como veremos en el análisis de complejidad después, esta propiedad acelerará el algoritmo, gracias a que el tamaño de los árboles que tendremos que considerar después decrecerá exponencialmente.
Para encontrar el centroide, seguiremos los siguientes pasos:
- Considerar el árbol arraigado en un nodo cualquiera
- Calcular los tamaños de los subárboles de cada nodo
- Desde la raíz ir hacia los nodos cuyo subárbol tiene tamaño mayor o igual que el tamaño total, sin ir hacia atrás
El último nodo en el que nos encontraremos será el centroide. Por ejemplo, en el siguiente árbol, lo encontraríamos siguiendo el camino marcado:
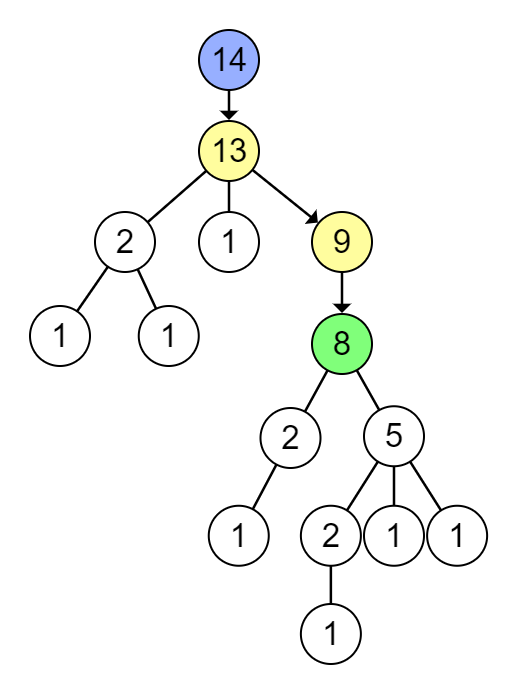
En la imagen, cada nodo tiene el tamaño de su subárbol, empezando en el azul acabamos encontrando el centroide, en verde.
A continuación podemos ver una posible implementación del algoritmo para encontrar el centroide:
#include<vector>
using namespace std;
typedef vector<int> vi;
typedef vector<vi> vvi;
vvi edges; // edges[v] contiene los vecinos de v
vi sizes; // vector para calcular los tamaños
// función que calcula el tamaño del subárbol de un nodo, dado su padre
// la raíz no tendrá padre (-1) y su tamaño será el de todo el árbol
int calcSize(int i, int parent) {
sizes[i] = 1;
for(int j: edges[i])
if(j != parent)
sizes[i] += calcSize(j, i);
return sizes[i];
}
int find_centroid() {
// arraigamos en el nodo 0 y calculamos tamaños
int totalSize = calcSize(0, -1);
// nos movemos hasta encontrar el centroide
int i = 0; // empezando desde la raíz
int prev = -1;
for(int x = 0; x < (int)edges[i].size(); ++x) {
int j = edges[i][x];
if(j != prev and sizes[j] > totalSize/2){
prev = i;
i = j;
x = -1;
}
}
return i;
}
Implementación genérica de un algoritmo con Centroid Decomposition
Tras encontrar el centroide, tendremos que solucionar la parte del problema que lo involucra (que será específico de cada problema), quitar el centroide y solucionar para cada uno de los árboles que hayan quedado.
Una forma cómoda de hacer esto es con un vector que marque si un nodo existe o no. Al principio todos existirán e iremos quitando los centroides. Y cambiando un poco la función $find\_centroid$ anterior, podremos hacer que nos encuentre los centroides de los siguientes árboles también. El código genérico de como sería un algoritmo que utiliza Centroid Decomposition sería el siguiente:
#include<vector>
using namespace std;
typedef vector<int> vi;
typedef vector<vi> vvi;
typedef vector<bool> vb;
vvi edges; // edges[v] contiene los vecinos de v
vi sizes; // vector para calcular los tamaños
vb exists; // vector que marca los nodos eliminados
int calcSize(int i, int parent) {
sizes[i] = 1;
for(int j: edges[i])
if(exists[j] and j != parent)
sizes[i] += calcSize(j, i);
return sizes[i];
}
// ahora tenemos un parámetro i, un nodo del árbol, que utilizaremos de raíz
int find_centroid(int i) {
// calculamos tamaños, del árbol en el que estamos
int totalSize = calcSize(i, -1);
int prev = -1;
for(int x = 0; x < (int)edges[i].size(); ++x) {
int j = edges[i][x];
if(exists[j] and j != prev and sizes[j] > totalSize/2){
prev = i;
i = j;
x = -1;
}
}
return i;
}
// función para resolver el problema para un árbol, dado un nodo cualquiera del árbol
// solve_centroid y merge_solutions dependen del problema a resolver
void solve_tree(int i) {
i = find_centroid(i);
// solucionar la parte del problema que depende del centroide
solve_centroid(i);
exists[i] = false; // quitar centroide
// y llamar recursivamente la función, para cada nuevo árbol
for(int j: edges[i])
if(exists[j])
solve_tree(j);
merge_solutions();
}
Ejemplo: Caminos de longitud $k$
Vamos a ver un ejemplo concreto del uso de Centroid Decomposition para solucionar el problema de encontrar cuántos caminos de longitud $k$ hay en un árbol, sin repetir aristas.
Para este problema, consideraremos cuántos caminos de longitud $k$ hay que pasen por el centroide y después sumaremos los caminos de longitud $k$ de los árboles resultantes de eliminar el centroide.
Y para saber cuántos caminos de longitud $k$ hay que pasen por el centroide, calcularemos cuantos puntos hay a distancia $1,2, \ldots, k$ del centroide, para cada subárbol. Con esto podremos calcular, para cada $l$ de $1$ a $k-1$, de cuántas formas podemos juntar un camino de longitud $l$ y uno de longitud $k-l$ (sin repetir aristas), ambos pasando por el centroide. Si a esto le sumamos los puntos a distancia $k$ del centroide, tendremos todos los caminos que pasan por este de longitud $k$.
La implementación de la solución entonces será la siguiente (omitimos las funciones ya implementadas previamente):
int k;
// función que calculará, para un subárbol, cuantos nodos hay de la raíz a distancia 1,...,k
// el resultado se almacenará en el vector dists
void calcDists(int i, int parent, int currDist, vi& dists) {
if(dists.size() <= currDist)
dists.push_back(0);
// contar el nodo actual
dists[currDist]++;
// y llamar recursivamente a los hijos
for(int j: edges[i])
if(exists[j] and j != parent and currDist < k)
calcDists(j, i, currDist+1, dists);
}
int solve_centroid(int i) {
// definimos un vector de vectores
// para cada hijo del centroide, tendremos un vector con cuantos nodos
// hay en su subárbol a cada distancia del centroide (v[i] será el número de nodos a distancia i)
vvi sonsDist;
for(int j: edges[i])
if(exists[j]) {
sonsDist.push_back({0});
// llamamos a la función auxiliar para llenar estos vectores
calcDists(j, i, 1, sonsDist.back());
}
vi totalDists; // suma de los vectores de los hijos
// cuantos nodos hay a cada distancia del centroide en total
for(vi& v: sonsDist) {
while(totalDists.size() < v.size())
totalDists.push_back(0);
for(int x = 0; x < v.size(); ++x)
totalDists[x] += v[x];
}
// ahora contamos cuantos caminos hay de longitud k pasando por el centroide
// los contaremos todos dos veces y luego dividiremos entre 2
int ans = k < totalDists.size() ? 2*totalDists[k] : 0;
for(vi& v: sonsDist) {
for(int x = 1; x < k and x < v.size(); ++x)
if(k-x < totalDists.size()) {
if((k-x) < v.size())
ans += v[x]*(totalDists[k-x] - v[k-x]);
else
ans += v[x]*totalDists[k-x];
}
}
ans /= 2;
return ans;
}
// función para resolver el problema para un árbol, dado un nodo cualquiera del árbol
int solve_tree(int i) {
i = find_centroid(i);
// solucionar la parte del problema que depende del centroide
int ans = solve_centroid(i);
exists[i] = false; // quitar centroide
// y llamar recursivamente la función, para cada nuevo árbol
for(int j: edges[i])
if(exists[j])
ans += solve_tree(j);
return ans;
}
En este caso no nos es necesario implementar $merge\_solutions$, porque solo necesitamos sumarlas y se puede hacer directamente cuando llamamos a $solve\_tree$.
Análisis de complejidad
Para encontrar el centroide tenemos que calcular previamente los tamaños de todos los subárboles, haciendo un DFS, que tiene complejidad $\mathcal{O}(n)$, donde $n$ es el número de nodos (como estamos en un árbol, hay $n-1$ aristas).
Y después resolveremos para los árboles más pequeños y tendremos que volver a hacer este cálculo. Para saber qué complejidad tiene en total hacer todo esto, distinguiremos los árboles en tipos. Diremos que el árbol original es de tipo $0$, los árboles resultantes de eliminar el primer centroide serán de tipo $1$, los siguientes serán de tipo $2$ y así sucesivamente. Hacer el DFS en cada uno de los árboles tiene complejidad $\mathcal{O}(n_i)$, donde $n_i$ es el número de nodos de ese árbol y si fijamos $k$ y nos fijamos en la suma de $n_i$ para los árboles de tipo $k$, vemos que será menor o igual que $n$ (el tamaño del árbol original). Por tanto, esta parte del algoritmo tendrá una complejidad de $\mathcal{O}(n \cdot t)$, donde $t$ es la cantidad de tipos de árboles que tenemos. Y si nos fijamos, tendremos como mucho $\log n$ tipos distintos, porque como estamos eliminando centroides, los árboles de tipo $k$ tendrán como mucho $n/2^k$ nodos y como el número de nodos en un árbol tiene que ser como mínimo 1, tenemos que $k \leq \log n$.
Por tanto, la complejidad de un algoritmo que utilice Centroid Decomposition será como mínimo $\mathcal{O}(n\log n)$.
Ahora nos falta añadir las complejidades de $solve\_centroid$ y $merge\_solutions$.
- Si estos tienen complejidad $\mathcal{O}(n)$. Este es el caso más habitual con el que nos encontraremos. Como $\mathcal{O}(n)$ es la misma complejidad que tiene hacer el DFS, no añadimos complejidad y en total seguiremos teniendo $\mathcal{O}(n\log n)$.
- Si tienen complejidad menor que $\mathcal{O}(n)$, la complejidad total también será $\mathcal{O}(n\log n)$.
- Si tienen complejidad mayor que $\mathcal{O}(n\log n)$, la complejidad total estará dominada por el cálculo de estas funciones en el primer árbol. La complejidad del algoritmo será la misma que la de $solve\_centroid$ y $merge\_solutions$.


Añadir nuevo comentario