En este manual veremos una estructura de datos, el Li Chao Tree, que si tenemos un conjunto de rectas, nos permitirá hacer rápido a las siguientes dos peticiones:
- Añadir una recta a nuestro conjunto
- ¿Cuánto es el mínimo de las rectas en un punto $x$ entero?
De hecho, no hace falta que sean rectas, sino que la misma estructura nos servirá para cualquier conjunto de funciones continuas que cada par de ellas intersequen en como mucho un punto, pero lo más común es que sean rectas.
Idea de la estructura
La estructura se basará en un árbol de segmentos donde cada hoja será un posible valor de $x$ (normalmente será entre $[1, 10^9]$ o entre $[-10^9, 10^9]$, después veremos como hacerlo para poder crear este árbol de segmentos) y cada nodo tendrá una recta que quizás será la mínima para alguno de sus hijos.
Para encontrar el mínimo valor en un punto, recorreremos el árbol de segmentos hasta su correspondiente hoja y nos quedaremos con el mínimo de las rectas de los nodos por los que hemos pasado.
Ahora, ¿cómo añadimos una nueva recta?
Si estamos en un nodo y nos fijamos en los rangos de valores de los dos hijos, el dibujo de las rectas (la que estamos añadiendo y la de ese nodo) será de la siguiente forma:
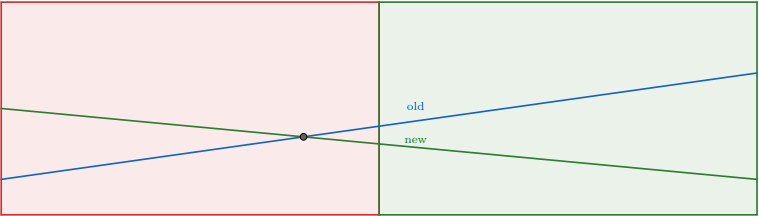
En uno de los hijos tendremos la intersección de las rectas, en este rango las dos rectas podrían ser el mínimo, y en el otro una recta siempre será menor que la otra. Entonces, en el nodo en el que estamos, nos quedaremos con la recta de valor más pequeño en el punto medio y al hijo que tenga la intersección de las dos rectas le añadiremos la otra.
Implementación
La implementación del árbol de segmentos, con punteros, será la siguiente:
#define x first
#define y second
typedef long long ll;
typedef pair<ll, ll> line;
ll applyFun(line f, ll x) { return f.x*x + f.y; }
struct node {
int a, b;
node *l, *r;
line f;
void addLine(line g) {
// nos quedamos con la menor en el punto medio
if(applyFun(g, (a+b)/2) < applyFun(f, (a+b)/2))
swap(f, g);
if(a == b-1)
continue;
// miramos si la intersección está en los rangos de los hijos
if(applyFun(g, a) < applyFun(f, a))
l->addLine(g);
if(applyFun(g, b) < applyFun(f, b))
r->addLine(g);
}
ll query(int x) {
if(a == b-1)
return applyFun(f, x);
if(x < (a+b)/2)
return min(l->query(x), applyFun(f, x));
else
return min(r->query(x), applyFun(f, x));
}
};
Si quisiéramos hacerlo con algún otro tipo de funciones que no sean rectas, la implementación sería la misma, pero cambiando la definición de $line$ y de $applyFun$.
También podríamos cambiar máximos por mínimos para tener la estructura que nos encuentre el máximo de las rectas para cierto $x$.
Ahora veremos como inicializar este árbol eficientemente.
Árbol de segmentos implícito
Hacer el árbol entero y almacenarlo en memoria suele ser inviable tanto por tiempo como por espacio. Por ejemplo, si nos pidieran un rango de valores de $[-10^9, 10^9]$, necesitaríamos unos $4 \cdot 10^9$ nodos, no es factible.
Por ello, utilizaremos lo que se conocen como árboles de segmentos implícitos. En un árbol de segmentos implícito, no creamos todos los nodos al principio, sino que solamente creamos los nodos que contengan información relevante y, si en algún momento hay algún nodo que antes era superfluo (no estaba creado), pero lo fuera a dejar de ser, en ese momento lo crearemos.
Teniendo esto en cuenta, la implementación de la estructura sería de la siguiente forma:
#define x first
#define y second
typedef long long ll;
typedef pair<ll, ll> line;
ll applyFun(line f, ll x) { return f.x*x + f.y; }
struct node {
int a, b;
node *l, *r;
line f;
// creamos un nodo con solo una recta
node(int x, int y, line g) {
a = x; b = y;
f = g;
// para los hijos no habría ninguna recta interesante, aparte de la que ya está en este nodo
l = r = nullptr; // no hace falta inicializarlos de momento
}
void addLine(line g) {
if(applyFun(g, (a+b)/2) < applyFun(f, (a+b)/2))
swap(f, g);
if(a == b-1)
continue;
if(applyFun(g, a) < applyFun(f, a)) {
// si el hijo al que le queremos pasar la recta no existe, lo creamos
if(l == nullptr)
l = new node(a, (a+b)/2, g);
else
l->addLine(g);
}
if(applyFun(g, b) < applyFun(f, b)) {
// si el hijo al que le queremos pasar la recta no existe, lo creamos
if(r == nullptr)
r = new node((a+b)/2, b, g);
else
r->addLine(g);
}
}
ll query(int x) {
// antes de recurrir a los hijos tendremos que mirar si existen
if(x < (a+b)/2)
return l ? min(l->query(x), applyFun(f, x)) : applyFun(f, x);
else
return r ? min(r->query(x), applyFun(f, x)) : applyFun(f, x);
}
};
Entonces, para inicializar nuestro árbol, crearemos únicamente la raíz, con una de las rectas, y después añadiremos todas las otras del conjunto inicial. Si nuestro conjunto fuera a empezar vacío, podemos inicializar la raíz con una recta que sabemos que nunca será la mínima, que será como si no existiera, como podría ser la recta $0\cdot x + \infty$.
Complejidad
Tanto para añadir una recta como para saber el mínimo en un punto, vamos a tener que ir desde la raíz del árbol hasta una de las hojas (como mucho) y el número de hojas que tenemos es la longitud del rango de valores que nos pueden preguntar. Por tanto, la complejidad final que tenemos será de $\mathcal{O}\left((n+q)log(R)\right)$ donde $n$ es el número de rectas que tiene el conjunto al principio, $q$ es el número de peticiones que nos harán y $R$ es la longitud del rango de valores que nos pueden preguntar. Y la cantidad de espacio que utilizaremos será $\mathcal{O}\left(n+q\right)$, ya que en cada nodo tendremos una recta distinta y como mucho tendremos $n+q$ rectas.
Esta estructura de datos suele ser bastante útiles para códigos de programación dinámica donde nos piden minimizar cierto valor y para hacerlo tenemos varias opciones que se pueden modelar como rectas. Entonces utilizaremos un Li Chao Tree.


Añadir nuevo comentario