Recursividad

Una función recursiva es aquella que se llama a sí misma. Por ejemplo:

void contador (int num) {
    if (num < 0) return;
    cout << num << endl;
    contador (num - 1);
}

Si ejecutamos la instrucción contador(3) se  mostrará por pantalla lo siguiente:

3
2
1
0

Haciendo un pequeño cambio, conseguimos que la función cuente hacia arriba.

void contador (int num) {
    if (num < 0) return;
    contador (num - 1);
    cout << num << endl;
}

Si ahora ejecutamos la instrucción contador (3) mostrará por pantalla:

0
1
2
3

La razón por la que ahora cuenta hacia arriba es porque la función se va llamando recursivamente hasta que num es -1 sin que se imprima ningún valor, y entonces mientras va volviendo a las llamadas anteriores se van ejecutando los comandos cout. Aquí se muestra un esquema de cómo se realiza la recursividad. La flecha indica en qué orden se ejecutan las instrucciones:

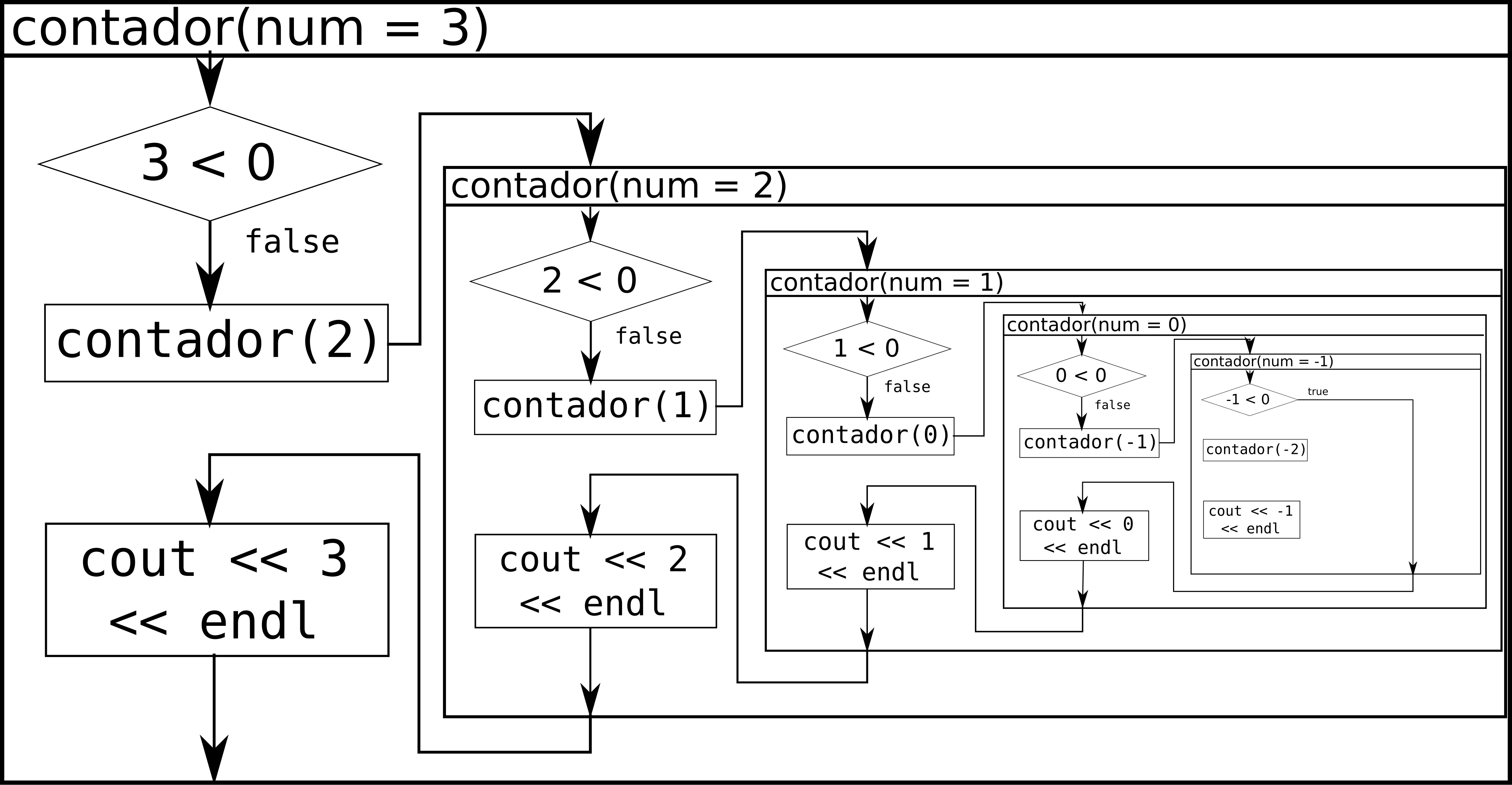
Nótese que la línea de código if(num < 0) return; evita que nuestra función se llame a sí misma infinitas veces (cosa que acabaría desbordando la memoria stack del ordenador, que es donde se guarda dónde tiene que volver el programa después de llamar a una función). El caso en el que paramos la recursión (num < 0, en este caso) se suele llamar caso base de la recursión.

Las funciones recursivas también pueden retornar valores, y eso se puede aprovechar para hacer cálculos. Por ejemplo, aquí hay una función que retorna el producto de los $n$ primeros números naturales:

int factorial(int n) {
    if (n == 0) return 1;
    return n * factorial(n-1);
}

(Al producto de los $n$ primeros números naturales se le llama n factorial). Y aquí hay otra que calcula los números de Fibonacci:

int fibonacci(int n) {
    if(n <= 1) return 1;
    return fibonacci(n-1) + fibonacci(n-2);
}

Estos ejemplos que hemos visto son muy sencillos y todos se pueden programar con soluciones que no utilicen recursividad, sólo bucles. De hecho, la mayoría de las cosas que se pueden hacer con recursividad se pueden hacer a través de bucles y vice versa, pero no siempre es igual de fácil plantearlo de una manera u otra. Esta disyuntiva entre un plantamiento iterativo y otro recursivo nos aparecerá en varias ocasiones.

Una de las situaciones en las que un planteamiento recursivo es más natural es cuando queremos generar todas las posibles combinaciones de algo. Por ejemplo, supongamos que queremos imprimir todas las palabras formadas por las letras ‘a’ y ‘b’ que tengan una longitud determinada. El siguiente código recursivo lo hace:

void rec(string s, int i) {
    if(i == n) {
        cout << s << endl;
    }
    else {
        rec(s+’a’, i+1);
        rec(s+’b’, i+1);
    }
}

Si llamamos rec(“”, 0) y tenemos n = 3 de variable global, lo siguiente se imprime en pantalla:

aaa
aab
aba
abb
baa
bab
bba
bbb