SCC y 2-SAT

Vamos a ver el algoritmo más importante sobre grafos dirigidos y su aplicación más popular. 

Para un grafo no dirigido ya sabemos encontrar sus componentes conexas usando un simple BFS o DFS. El concepto de componente conexa no es tan sencillo en grafos dirigidos: que de A se pueda ir a B no implica que de B se pueda ir a A. En los grafos dirigidos hablamos entonces de componentes fuertemente conexas (o SCC por sus siglas en inglés). Una SCC es un conjunto (maximal) de vértices tal que de dos cualesquiera podemos viajar de uno al otro en ambas direcciones.

Pongamos por ejemplo este grafo:

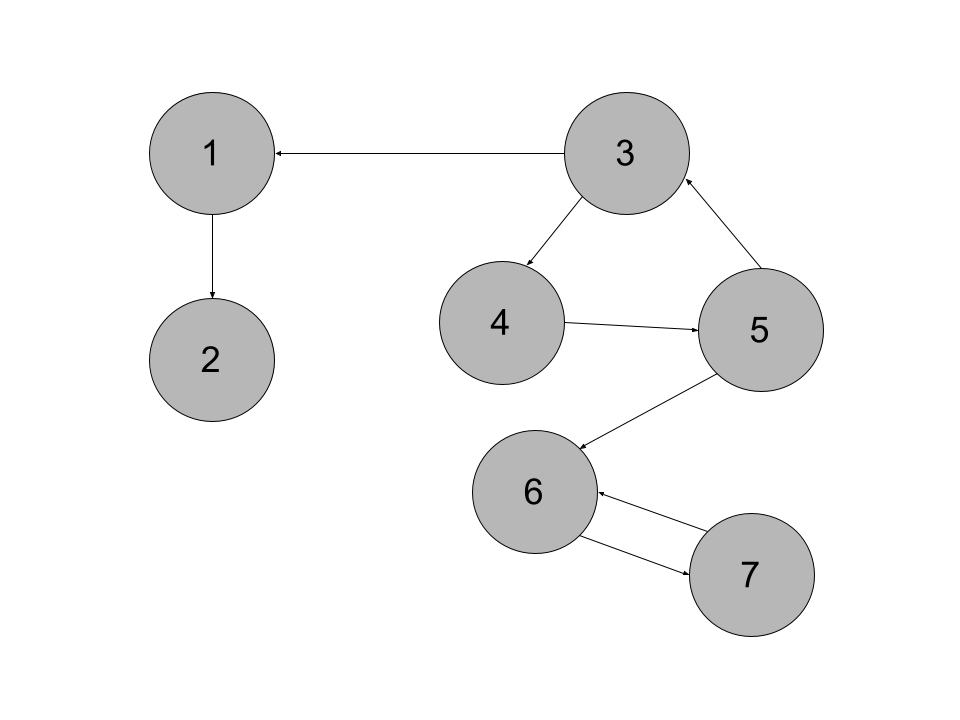
Sus componentes conexas son: [1], [2], [3,4,5], [6,7].

El algoritmo para encontrarlas se basa en el concepto ya visto de DFS tree, pero generalizado para grafos no dirigidos. Realicemos un DFS en el grafo anterior pero marcando también el tiempo de "salida" de cada vértice: es decir, ordenaremos los vértices según el orden en que los dejemos de explorar:

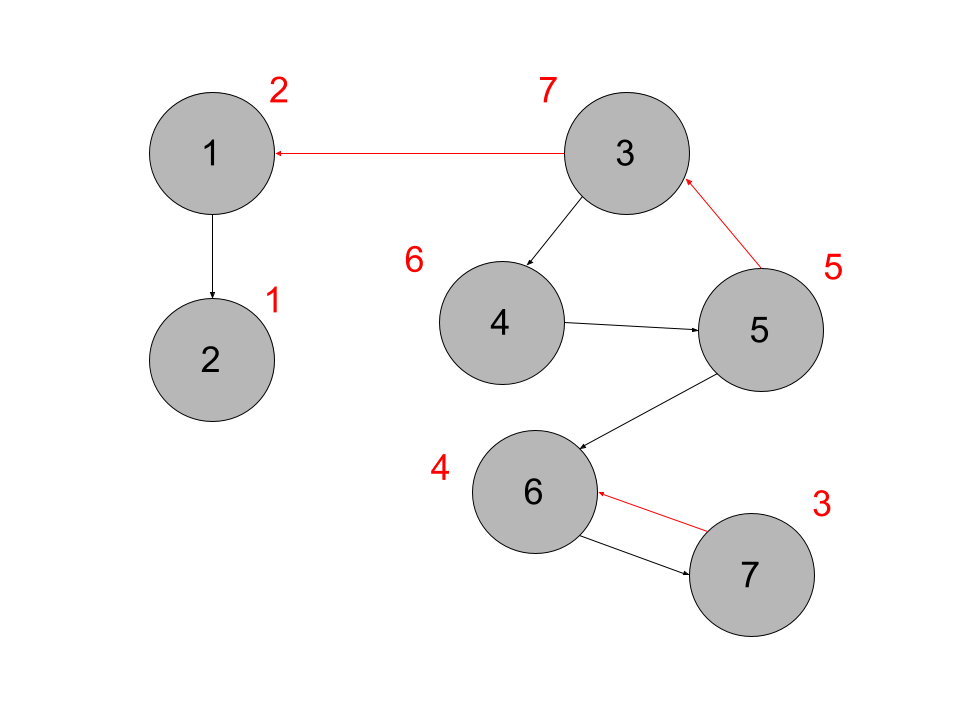
Hemos marcado los tiempos de salida en rojo así como las back-edges. Nos fijamos ahora que si un vértice tiene un tiempo de salida mayor que otro quiere decir que podemos acceder de el primero al segundo o que no podemos acceder de uno al otro (esta demostración se puede hacer formalmente pero no la incluiremos, lo puedes intentar demostrar). Esto nos da una forma de encontrar los SCC. Si empezamos por el vértice con mayor tiempo de salida sabemos que puede acceder al resto, y por lo tanto los vertices que estarán en su mismo SCC son los que también pueda acceder a él.

Queda saber cómo buscar los vértices que pueden acceder a este vértice. Para ello es suficiente con hacer un DFS desde este vértice pero no con nuestro grafo original G si no con G^T es decir, el grafo con las aristas giradas (usamos la notación de traspuesto porque sus matrices de adyacencia son traspuestas la una de la otra). 

Por lo tanto para encontrar los SCC tenemos que hacer DFS desde cada vértice desde el que tiene el tiempo de salida mayor y los vértices que encontremos en cada DFS estarán en un mismo SCC.

Podemos ver una implementación de esto:

vector<vector<int>> G, G_trans; // lista de adyacencia del grafo y del grafo traspuesto
vector<bool> visitado;
vector<int> orden; // nos guardaremos los vertices ordenados por tiempo de salida
vector<int> componentes; // componentes[u] == componentes[v] sii estan en el mismo SCC
int n; // numero de vertices

void dfs1(int v) {
    visitado[v] = true;
    for (int i = 0; i < G[v].size(); ++i) {
        int u = G[v][i];
        if (!visitado[u])
            dfs1(u);
    }
    // nos apuntamos que hemos salido
    orden.push_back(v);
}

void dfs2(int v, int componente) {
    componente[v] = componente;
    for (int i = 0; i < G_trans[v].size(); ++i) {
        int u = G_trans[v][i];
        if (componente[u] == -1)
            dfs2(u, componente);
    }
}

// devuelve el numero de SCC
int SCC() {
    visitado = vector<bool>(n, false);
    for (int i = 0; i < n; ++i)
        if (!visitado[i])
            dfs1(i);
    reverse(orden.begin(), orden.end());

    componentes = vector<int>(n, -1);
    int num_componentes = 0;
    for (int i = 0; i < n; ++i)
        if (componente[orden[i]] == -1) {
            dfs2(orden[i], num_componentes);
            num_componentes++;
        }

    return num_componentes;

}

 

2-SAT

Decimos que una fórmula lógica es un problema 2-SAT si tiene la forma (x_a v x_b) & ... &  (x_c v x_d). Las x son variables que pueden ser cierto o falso (y que pueden aparecer negadas, lo que indicaremos como x_a) y v quiere decir OR lógico y & and lógico. Queremos saber si hay alguna forma de dar valor a las variables x tal que la forma evalúe a cierto. Vemos que esto es equivalente a decir que en cada paréntesis una de las dos variables sea cierta (o falsa si esta negada). Si en los paréntesis hubiese más de 2 variables este sería un problema NP-completo.

Pero si los paréntesis solo tienen dos variables podemos resolverlo usando el algoritmo de SCC:

Para empezar nos construiremos un grafo G. Los vértices de este grafo G serás las variables x y sus negaciones. Si tenemos n variables tendremos 2n vértices. Ahora, si en un paréntesis tenemos la expresión x_a v x_b añadiremos una arista de x_a a x_b y una arista de x_b a x_a. Hay que entender estas aristas como implicaciones: que x_a sea falso quiere decir que necesitamos que x_b sea cierto para que el paréntesis se cumpla.

Ahora con este grafo ya podemos resolver el problema: cómo hemos dicho las aristas hay que entenderlas como implicaciones. Qué pasa si x_a implica x_a y a su vez x_a  implica x_a? Que estamos en una situación imposible: que x_a sea falso implica que es cierto y viceversa. Si esto sucede para alguna variable el problema no tendrá solución. Si esto no sucede para ninguna variable el problema tiene solución (ejercicio). 

Ahora para saber si suceden estas dobles implicaciones tiene una traducción directa en nuestro grafo: que una variable y su negación estén en la misma SCC (convéncete de esto). 

Por lo tanto para resolver el problema es suficiente construir el grafo, correr el algoritmo anterior y comprobar la condición. Todo esto se puede hacer en tiempo lineal!