Una de las estrucutras de datos más útiles cuando tratamos problemas sobre prefijos son los Tries (también llamados árboles de prefijos). Esta estructura nos permite mantener propiedades sobre elementos que comparten prefijo. En particular, la estructura consiste en representar un conjunto de elementos a través de un árbol, donde cada nodo representa un carácter, el número de nodos es mínimo y todas las palabras aparecen como caminos en el árbol empezando por la raíz. Por ejemplo, el Trie correspondiente a las palabras {pan, pin, te, test, tres y tren} sería:
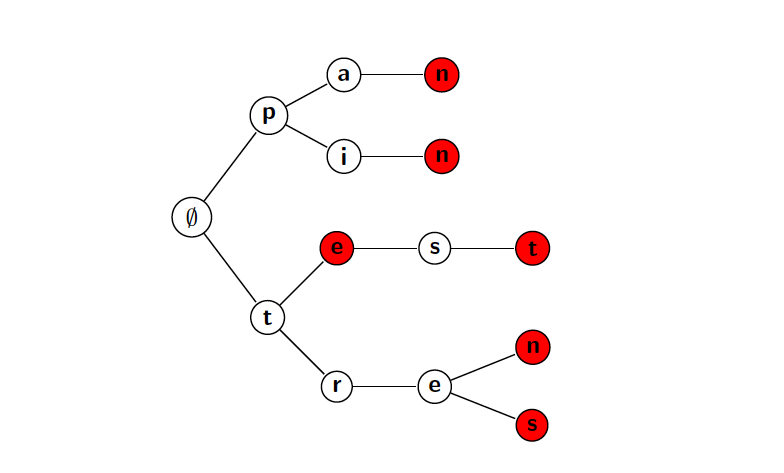
Nótese que todas las hojas de un Trie corresponden a elementos del conjunto, pero no todos los elementos terminan en una hoja (en el ejemplo anterior, "te" no termina en una hoja).
Para representar un Trie, utilizaremos punteros. Un puntero es una variable que guarda la dirección de memoria en la que se encuentra una variable en concreto. El tipo de un puntero depende de la variable a la que apunta, y se denota como el tipo de la variable seguida de un asterisco. Además, la dirección de memoria donde se guarda una variable se puede obtener usando el operador "&" precediendo a la variable. Por ejemplo, en
int* direccion = &numero
direccion es un puntero que apunta a enteros (int*). En particular, direccion apunta en este momento a la dirección de memoria donde está guardada la variable numero (&numero). Los punteros pueden apuntar a "nada" si se les asigna como valor nullptr. Además, si tenemos un puntero apuntando a una estructura, lo podemos inicializar usando "new" y podemos acceder a sus elementos con el operador "->". Por ejemplo:
struct Alumno{
string nombre;
int edad;
};
Alumno Pablo = {"Pablo", 16};
Alumno* puntero = & Pablo;
puntero -> edad = 17;
Alumno* Cristina = new Alumno {"Cristina", 18};
Una vez hecha esta introducción, veamos tres implementaciones de Tries:
Trie con arrays
La implementación más simple consiste en tener un nodo raíz y que cada nodo tenga tantos punteros como hijos pueda tener (inicialmente todos nullptr). Al añadir palabras al trie, iremos a la posición a la que apunta el puntero correspondiente al carácter que tengamos, o lo crearemos si no existe ese nodo.
Veamos un ejemplo de como crear un Trie:
#include <iostream>
using namespace std;
struct Nodo{
Nodo* hijos[26] = {nullptr};
int final = 0;
};
// Añade la palabra dada empezando desde la posición indice,
// teniendo en cuenta de que nos encontramos en el nodo Trie.
void add(Nodo* Trie, string& palabra, int indice){
// Si ya hemos añadido toda la palabra, indicar que habíamos
// acabado el pa posición anterior.
if (palabra.size() == indice){
Trie -> final += 1;
return;
}
int caracter = palabra[indice] - 'a';
if (not Trie -> hijos[caracter]) {
// Si Trie no tiene un nodo hijo que represente el carácter
// palabra[indice], crea el nodo.
Trie -> hijos[caracter] = new Nodo;
}
// Sigue añadiendo la palabra empezando por el siguiente carácter.
add(Trie -> hijos[caracter], palabra, indice + 1);
}
int main() {
// Crea el nodo raíz del Trie.
Nodo* raiz = new Nodo;
// Añade la palabra tren al Trie:
string palabra = "tren";
add(raiz, palabra, 0);
}
En este caso para cada nodo nos guardamos el número de palabras que terminan en ese nodo y, el nodo en cuestión apunta a todos sus hijos (que son otros nodos).
Notas:
- Es la implementación de Trie con menor coste en tiempo de acceso a un hijo: $\mathcal{O}(1)$
- Es la implementación de Trie con mayor coste en memoria: $\mathcal{O}(\alpha \cdot n)$, donde $n$ es el número de nodos y $\alpha$ el mayor número de hijos que un nodo puede tener (en general $\alpha = 26$, el número de letras en el alfabeto inglés).
Trie con unordered maps
Una opción similar, pero con menor coste en memoria, consiste en usar unordered maps en vez de arrays para guardar a los hijos de cada nodo. De este modo, solo hay que inicializar aquellos nodos que realmente existan.
#include <iostream>
#include <unordered_map>
using namespace std;
struct Nodo{
unordered_map <char, Nodo*> hijos;
int final = 0;
};
// Añade la palabra dada empezando desde la posición indice,
// teniendo en cuenta de que nos encontramos en el nodo Trie.
void add(Nodo* Trie, string& palabra, int indice){
// Si ya hemos añadido toda la palabra, indicar que habíamos
// acabado el pa posición anterior.
if (palabra.size() == indice){
Trie -> final += 1;
return;
}
char caracter = palabra[indice];
if (Trie -> hijos.find(caracter) == Trie -> hijos.end()) {
// Si Trie no tiene un nodo hijo que represente el carácter
// palabra[indice], crea el nodo.
Trie -> hijos[caracter] = new Nodo;
}
// Sigue añadiendo la palabra empezando por el siguiente carácter.
add(Trie -> hijos[caracter], palabra, indice + 1);
}
int main() {
// Crea el nodo raíz del Trie.
Nodo* raiz = new Nodo;
// Añade la palabra tren al Trie:
string palabra = "tren";
add(raiz, palabra, 0);
}
Notas:
- Esta implementación de Trie tiene un coste en tiempo de acceso a un hijo de $\mathcal{O}(1)$, sin embargo, es ligeramente más lenta que con arrays, pues tiene un coste con una constante mayor.
- Esta implementación de Trie tiene un coste en memoria de $\mathcal{O}(n)$, donde $n$ es el número de nodos que tiene el Trie.
Trie de hermanos
Casi siempre tendremos suficiente con alguna de las anteriores 2 implementaciones. Sin embargo, en casos que haya que rascar mucho en memoria o en casos con memoria ajustada donde queramos rascar en tiempo y sepamos que tendremos un Trie extremadamente poco denso, puede ser util la siguiente representación. En este caso, cada nodo tendrá como mucho un hijo y, como mucho, un hermano. La idea es que si un nodo $v$ ya tiene un hijo $u$ con un carácter distinto al nuestro, y nosotros también hemos de ser hijos de $v$, entonces pasaremos a ser hermano de $u$ (o hermano del hermano de $u$ si este ya tiene hermano, y así sucesivamente). Una posible implementación sería:
#include <iostream>
#include <unordered_map>
using namespace std;
struct Nodo{
char caracter;
int final;
Nodo* hijo;
Nodo* hermano;
};
Nodo* busca_hermano(Nodo* Trie, char caracter){
if (Trie -> caracter == caracter) return Trie;
if (not Trie -> hermano){
Trie -> hermano = new Nodo {caracter, 0, nullptr, nullptr};
}
return busca_hermano(Trie -> hermano, caracter);
}
// Añade la palabra dada empezando desde la posición indice,
// teniendo en cuenta de que nos encontramos en el nodo Trie.
void add(Nodo* Trie, string& palabra, int indice){
// Si ya hemos añadido toda la palabra, indicar que habíamos
// acabado el pa posición anterior.
if (palabra.size() == indice){
Trie -> final += 1;
return;
}
char caracter = palabra[indice];
if (not Trie -> hijo) {
// Si Trie no tiene un nodo hijo que represente el carácter
// palabra[indice], crea el nodo.
Trie -> hijo = new Nodo {caracter, 0, nullptr, nullptr};
add(Trie -> hijo, palabra, indice + 1);
}
else {
// Sigue añadiendo la palabra empezando por el siguiente carácter.
add(busca_hermano(Trie -> hijo, caracter), palabra, indice + 1);
}
}
int main() {
// Crea el nodo raíz del Trie.
Nodo* raiz = new Nodo {'!', 0, nullptr, nullptr};
// Añade la palabra tren al Trie:
string palabra = "tren";
add(raiz, palabra, 0);
}
Notas:
- Es muy recomendable usar alguna de las otras representaciones antes que esta, ya que, en general, tiene un coste de acceso mayor que las demás y suele llevar más tiempo implementar códigos con esta versión.
- Esta implementación tiene un coste en tiempo de acceso a un hijo de $\mathcal{O}(\alpha \cdot n)$, es por eso que solo se recomienda en Tries muy poco densos. En algunos casos extremos puede llegar a ser más rápido que la versión con unordered map, debido al overhead de esa clase.
- Esta implementación de Trie es la que tiene menor coste en memoria. El coste es $\mathcal{O}(n)$, sin embargo, ocupa menos que la segunda versión debido a sobrecostes que tiene la clase unordered_map.


Añadir nuevo comentario