Un algoritmo voraz (greedy) es un algoritmo que encuentra una solución globalmente óptima a un problema a base de hacer elecciones localmente óptimas. Es decir: el algoritmo siempre hace lo que “parece” mejor en cada momento, sin tener nunca que reconsiderar sus decisiones, y acaba llegando directamente a la mejor solución posible. Es una técnica bastante abstracta que se ilustra mejor con un ejemplo:
Ejemplo 1 (Final OIE 2018):
Hay $M$ $(M \leq 10^5)$ farolas en las posiciones $y_1, \ldots, y_M$ de una recta y $N$ $(N \leq 10^5)$ puntos $x_1, \ldots, x_N$. Cada farola tiene un radio de iluminación $r_i$, tal que la i-ésima farola ilumina puntos en el intervalo $[y_i-r_i, y_i+r_i]$. Se quiere encender el mínimo número de farolas tales que cada uno de los $N$ puntos $x_1, \ldots x_N$ esté iluminado por al menos una farola. Encuentra este mínimo número.
Para resolver este problema, nos imaginamos los puntos y las farolas en la recta, ordenados de izquierda a derecha. Fijémonos en el primer punto (por la izquierda): tendrá que haber una farola que lo ilumine. Entre todas las que lo pueden iluminar, ¿cuál es la mejor? Claramente no nos importa cuánto cubra por la izquierda de ese punto, ya que no hay ningún punto a la izquierda de ese que nos interese iluminar. Sin embargo, sí que nos interesa que cubra lo máximo posible por la derecha. Por tanto, entre las farolas que cubren el primer punto, elegimos una cuyo alcance por la derecha sea máximo.
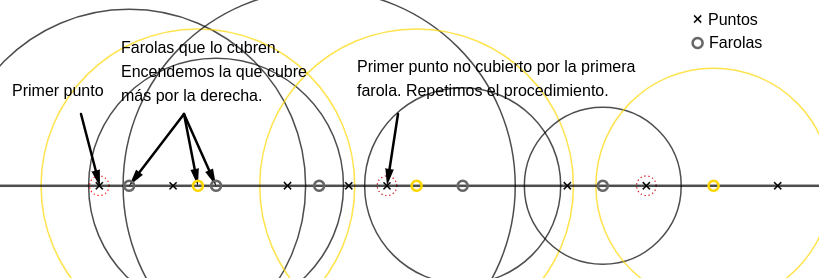
Una vez hemos elegido esta farola, algunos puntos adicionales quedarán cubiertos por ella. Pasamos al siguiente punto por la izquierda que no esté cubierto. Nuevamente tenemos que elegir una farola que lo cubra y otra vez no nos importa cuánto cubra por la izquierda, ya que todos los puntos a la izquierda de él ya están iluminados por la otra farola. Así que elegimos la que más cubra por la derecha. Pasamos al siguiente punto que no está iluminado y repetimos la idea hasta que tenemos todos los puntos iluminados. Esta solución se puede implementar fácilmente en $\mathcal{O}(N \log N + NM)$: se ordenan los puntos en $\mathcal{O}(N \log N)$ y para cada uno de los puntos que vayamos procesando iteramos por todas las farolas en $\mathcal{O}(M)$ y entre las que lo cubren elegimos la que $y_i+r_i$ sea máximo. (En casos normales procesaremos bastante menos que $N$ puntos, como se puede ver en el diagrama, en el que sólo procesamos 3 de 8. Sin embargo, en el peor de los casos procesamos $N$, y de aquí la complejidad $\mathcal{O}(NM)$).
Ejercicio 1. Para obtener la puntuación máxima en el problema hay que mejorar la implementación para que la complejidad sea $\mathcal{O}(N \log N + M \log M)$: dejamos los detalles al lector. Puedes enviar tu programa y probar si funciona aquí.
Nótese que este algoritmo sigue el proceso de “elegir la mejor opción en cada momento”: esta es la idea principal en la que se basan los algoritmos voraces. Veamos otro ejemplo:
Ejemplo 2 (Cambio de monedas):
Dada una cantidad de dinero (en euros), dar el mínimo número de monedas (con las denominaciones usuales: 1c, 2c, 5c, 10c, 20c, 50c, 1€, 2€) que sume esa cantidad.
La idea aquí es que, para minimizar el número total de monedas que utilizamos, queremos incluir las monedas de máximo valor que podamos. Por ejemplo, si tenemos 5,79€, vamos a querer usar dos monedas de 2€. Lo que queda es 1,79€ y la siguiente moneda más grande es de 1€, así que la incluimos. Después la moneda de más valor con valor menor a 0,79€ es la de 50 céntimos, después añadimos una de 20, después una de 5 y después dos de 2. Al final tenemos:
$$5,79 = 2,00 + 2,00 + 1,00 + 0,50 + 0,20 + 0,05 + 0,02 + 0,02$$
con un total de 8 monedas. No se puede obtener esa suma con menos monedas. El algoritmo que seguimos se puede implementar sencillamente con este código:
//int suma tiene la suma que queremos representar
//vector<int> denominaciones tiene las denominaciones de las monedas ordenadas de mayor a menor
int i = 0;
int monedas = 0;
while (suma > 0) {
monedas += suma / denominaciones[i];
suma %= denominaciones[i]; //resto de la división entera
++i;
}
//monedas tiene el número mínimo de monedas necesarias.
Parece sencillo, ¿verdad? Ahora supongamos que vamos a un país lejano con una moneda diferente. Vienen en denominaciones de 1, 3 y 4 unidades. Supongamos que hay que encontrar el mínimo número de monedas que sumen 6. El algoritmo voraz eligiría primero la de 4, y luego dos de 1… pero la respuesta correcta son dos monedas, 3+3. Nuestro algoritmo no funciona en este caso. (Una solución correcta al problema de cambio de monedas para cualquiera denominaciones se expone en el manual de Programación Dinámica)
Esta es una lección importante: los algoritmos voraces no suelen dar la respuesta correcta. Aunque tengamos una idea que creamos que puede funcionar, no siempre podemos fiarnos de nuestra intuición y tenemos que intentar buscar contraejemplos para ver si falla en algún caso. Para esto puede ser útil escribir un programa de búsqueda completa que encuentre la solución correcta de forma garantizada y comparar sus resultados con los del algoritmo voraz para casos pequeños. Si creemos que nuestro algoritmo es correcto, podemos intentar demostrar su corrección: aunque no sea una demostración completamente formal, se puede pensar en por qué el algoritmo da la respuesta óptima.
Ejercicio 2: El algoritmo voraz para el problema de cambio de monedas sí que da la respuesta correcta en el caso de que trabajemos con las monedas de euros normales. ¿Por qué? ¿Qué condiciones sobre las denominaciones de las monedas son suficientes para que el algoritmo voraz funcione en este problema?
A continuación se incluye un razonamiento sobre la corrección del algoritmo voraz para el problema del Ejemplo 1. Ilustra la técnica de demostración por contradicción, muy útil para comprobar que un algoritmo voraz da la solución óptima: suponemos que tenemos una solución mejor que no es la dada por el algoritmo y llegamos a una situación contradictoria.
Supongamos que tenemos una solución que utiliza menos farolas que la construida por nuestro algoritmo. Entonces, en esta solución óptima, hay al menos una farola que estaba encendida en la solución dada por el algoritmo voraz y aquí está apagada. Elegimos la que esté más a la izquierda entre estas. Consideremos el primer punto $x_i$ que no está iluminado por las farolas anteriores elegidas por el algoritmo voraz. En la solución óptima hay una farola que lo ilumina, distinta a la del algoritmo voraz. Si apagamos esa farola y encendemos la que falta del algoritmo voraz, ningún punto deja de estar iluminado: los puntos a la izquierda de $x_i$ están todos iluminados por las otras farolas y la farola elegida por el algoritmo voraz cubre más a la derecha que cualquier otra farola que cubra $x_i$: en particular, cubre más a la derecha que la que teníamos encendida en nuestra solución óptima, así que ningún punto que antes estaba iluminado deja de estarlo. Así, hemos construido otra solución con menos farolas que la del algoritmo voraz, pero esta vez la primera farola que falta está más a la derecha. Podemos repetir este razonamiento: como el número de farolas es finito y cada vez la primera farola “diferente” está más a la derecha en cada solución óptima que vamos construyendo sucesivamente, al final acabaremos encendiendo todas las farolas que estaban dadas por nuestro algoritmo voraz pero habremos mantenido constante el número de farolas de la solución, cosa que es una contradicción con nuestra suposición de que la solución tenía menos farolas que la dada por el algoritmo voraz.


Añadir nuevo comentario