Vamos a ver en este artículo un uso más profundo del algoritmo DFS. En particular, nos vamos a fijar en la traza que deja si observamos como visita los vertices de nuestro grafo (no dirigido) y que información nos puede dar esto sobre propiedades estructurales del grafo.
DFS tree
El concepto en el que se basaran las idea de este tutorial es el DFS tree. Formalmente un DFS tree de un grafo (se entiende conexo) es el árbol que se obtiene al considerar solo las aristas que son visitadas por un recorrido de DFS para saltar entre vertices. Por ejemplo, consideremos el siguiente grafo:
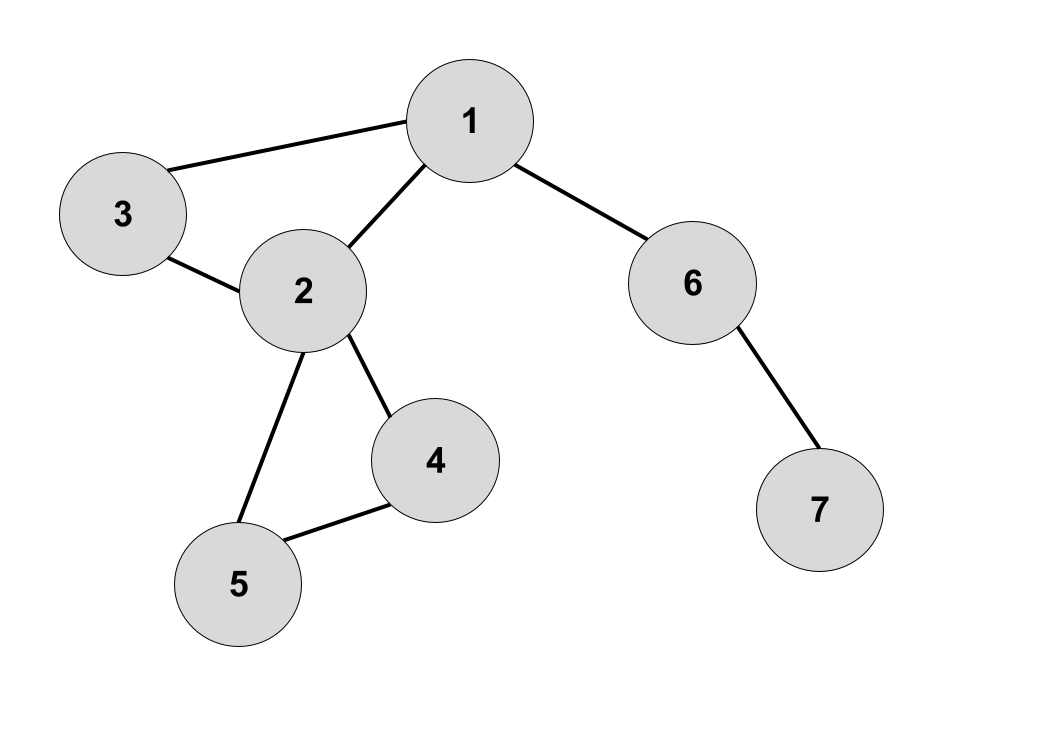
Si hacemos un recorrido en DFS empezando por el vértice 1 y visitando primero los vertices con menor número, encontraremos lo siguiente:
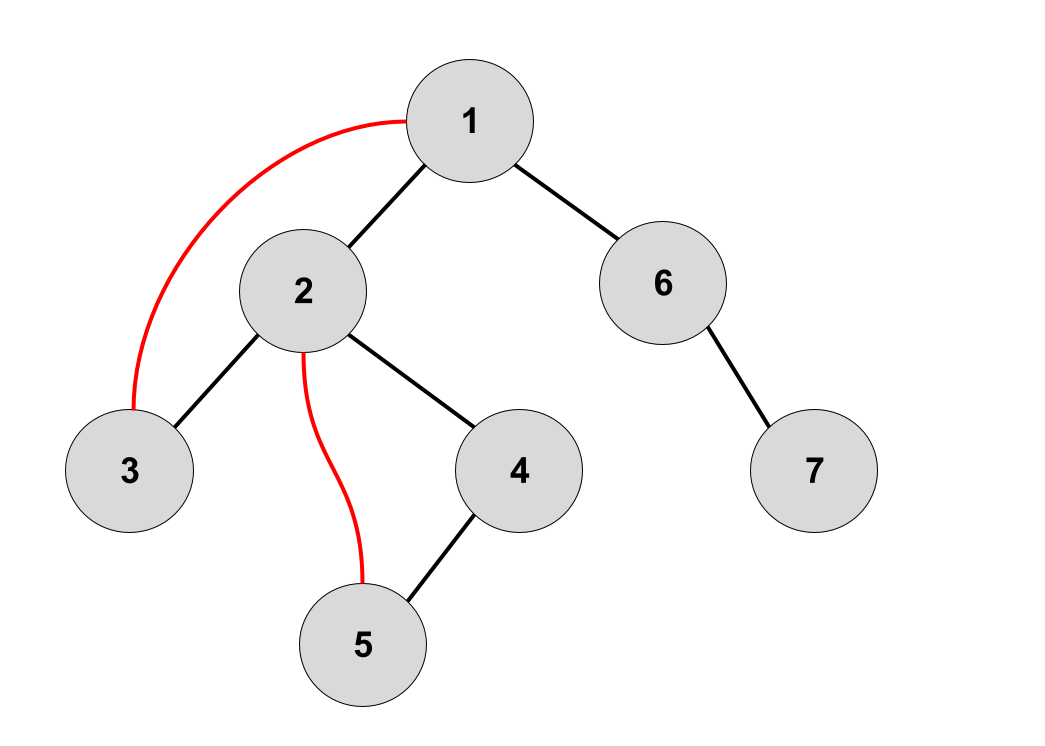
Las aristas pintadas de negro son aquellas que pertenecen al DFS tree, son aquellas que se han utilizado para explorar. El primer paso del DFS ha sido viajar del vértice 1 al 2 por la arista que los une. En cambio, la arista entre 1 y 3 ha sido visitada desde el vértice 3, pero se no se ha vuelto a visitar el vértice 1 ya que ya estaba marcado como visitado. A las aristas negras las llamaremos tree-edges y a las de rojo, que no pertenecen al árbol, las llamaremos back-edges, ya que van "hacia detrás" del árbol.
Es importante también el concepto de ancestro: decimos que un vértice a es un ancestro de b si b esta en el subárbol de a, es decir, b ha sido encontrado mientras se exploraba las aristas de a. Por ejemplo, 1 es ancestro de todos los otros vértices. 2 es ancestro de 3, 4 y 5 pero no de 6 o 7. 3,5,7 no son ancestro de nadie. En particular, llamamos padre al vértice que se estaba visitando cuando se ha descubierto otro. 1 es el padre de 2 y 6. 4 es el padre de 5 y 7 no es el padre de nadie.
Vamos a ver dos algoritmos que se basan en estos conceptos.
Articulation points
El primer problema que vamos a resolver es encontrar los articulation points (puntos de articulación) de nuestro grafo. Llamamos articulation points a aquellos vértices que si los eliminamos desconectan el grafo. En nuestro grafo anterior, los vértices 1, 2 y 6 son los articulation points. Podemos ver que si eliminamos el vértice 1 el grafo pasa a tener 2 componentes conexas, pero eliminar el vértice 3 no afecta a la conexión del resto del grafo.
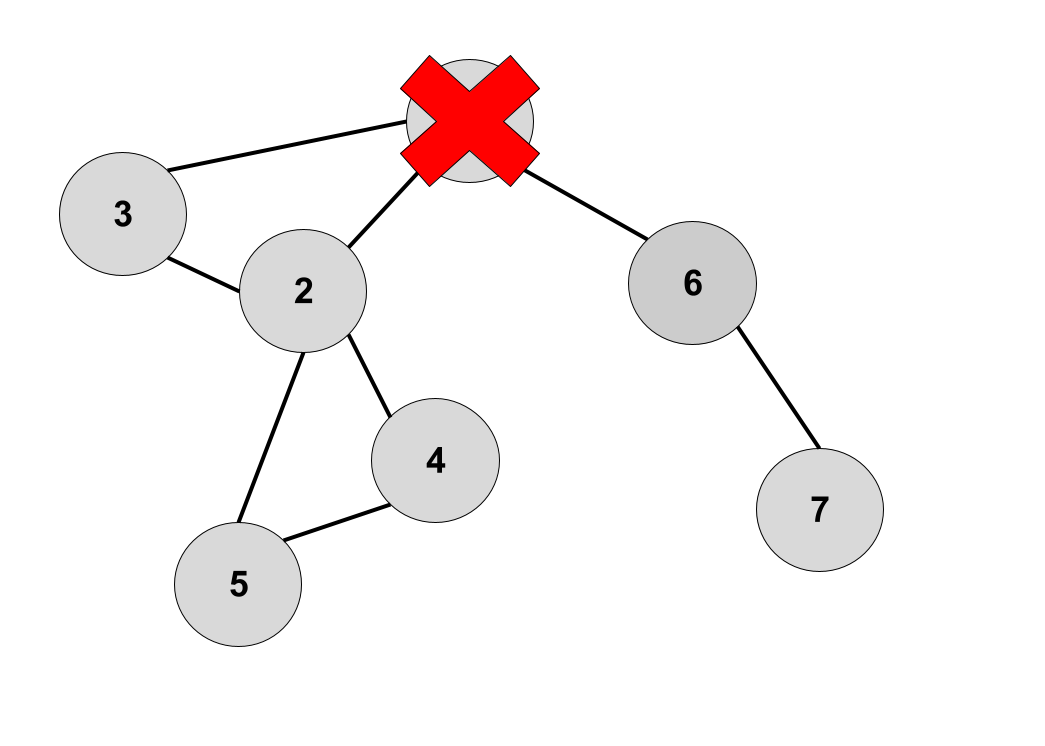
Vamos a ver qué tiene que cumplir un vértice para ser un articulation point, pero no razonaremos sobre el grafo directamente, si no sobre el DFS tree.
Observamos que para el vértice del que sale el DFS tenemos una condición sencilla. Si es el padre de más de un vértice (como en nuestro ejemplo), podemos asegurar que si lo borramos el grafo se desconectará. En caso contrario, es fácil observar que no sera un articulation point (puedes construir el DFS tree empezando desde el vértice 5 de nuestro grafo de ejemplo para convencerte).
Para el resto de vértices la condición tiene que ver con los back-edges de su descendencia. Fijémonos en el vértice 2 de nuestro árbol: vemos que tiene un hijo 3 con un back-edge que apunta "hacia detrás" de 2. Eso quiere decir que aunque borremos el vértice 2, el vértice 3 seguirá conectado al resto del grafo gracias a este back-edge. En cambio, también tiene a 4 como hijo. En el subárbol de 4 y 5 no hay ningún back-edge que vaya "hacia detrás" de 2. Esto quiere decir que si borramos el vértice 2, el vértice 4 y 5 quedaran aislados. Tenemos por lo tanto dos condiciones para comprobar si un vértice es un articulation point.
- Para el vértice donde se empieza el DFS hay que ver si tiene más de un hijo.
- Para el resto de vértices hay que ver si para alguno de sus hijos ese subárbol no tiene ningún back-edge que vaya "hacia detrás" del vértice.
Una posible implementación para este problema seria:
// ap = articulation points, ap[i] = True sii i es un articulation point
// disc[u] = posicion en la que se ha visitado
// low[u] = backedge que apunta mas arriba del subarbol de u
// esta variable nos servira para saber en que orden visitamos los nodos
int nodos_visitados = 0;
// devuelve el numero de hijos para comprobar la condicion 1
int dfs (int v, int padre) {
int numero_hijos = 0;
low[v] = disc[v] = nodos_visitados;
nodos_visitados++;
for (int i = 0; i < G[v].size(); ++i){ //iteramos por todos los vecinos
int u = G[v][i];
if (u == p) continue; // no queremos visitar el padre
if (!disc[u]) { // vamos a abrir un subarbol con un nodo que todavia no habiamos visitado
numero_hijos++;
dfs(u, v); // visitamos el hijo
if (disc[v] <= low[u]) // comprobamos la segunda condicion
ap[v] = 1;
low[v] = min(low[v], low[u]); // actualizamos low[v] para reflejar los backedges del subarbol
}
else { // nos encontramos con un backedge y actualizamos low[v] acordemente
low[v] = min(low[v], disc[u]);
}
}
return numero_hijos;
}
void AP() {
ap = low = disc = vector<int>(G.size(), 0);
nodos_visitados = 0;
// iteramos por si el grafo por si no es conexo visitarlo todo
for (int u = 0; u < adj.size(); u++)
if (!disc[u])
ap[u] = dfsAP(u, u) > 1; // condicion 1
}
Bridges
Ahora vamos a ver lo que llamamos puentes o bridges. Es un concepto muy parecido al anterior, pero nos centramos no en los vértices sino en las aristas. Diremos que una arista es un puente si al borrarla desconectamos el grafo. En nuestro ejemplo anterior la arista entre 1 y 6 es un bridge:
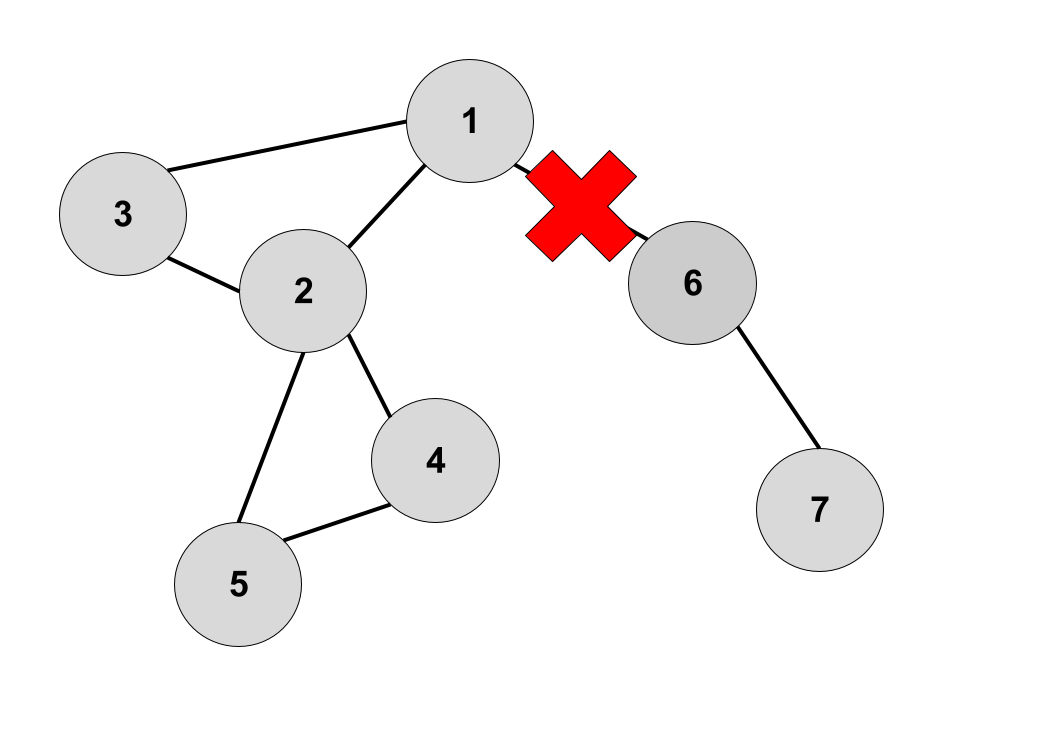
También lo es la arista entre 6 y 7 pero ninguna de las otras.
Volvamos a analizar qué propiedad tiene que tener una bridge fijándonos en el DFS tree. La primera observación sencilla es que un back-edge nunca es un bridge. Ahora sobre las aristas del DFS tree tenemos una condición muy parecida a la condición 2 del problema anterior: una arista sera un bridge si en su subárbol no hay ningún back-edge que vaya hacia el vértice que estamos visitando o más hacia detrás (convéncete de este hecho mirando el DFS tree de ejemplo).
Con esta condición podemos resolver este problema de forma muy parecida al anterior:
// bridges = una lista con todos los bridges
// disc[u] = posicion en la que se ha visitado
// low[u] = backedge que apunta mas arriba del subarbol de u
// esta variable nos servira para saber en que orden visitamos los nodos
int nodos_visitados = 0;
void dfs (int v, int padre) {
low[v] = disc[v] = nodos_visitados;
nodos_visitados++;
for (int i = 0; i < G[v].size(); ++i){ //iteramos por todos los vecinos
int u = G[v][i];
if (u == p) continue; // no queremos visitar el padre
if (!disc[u]) { // vamos a abrir un subarbol con un nodo que todavia no habiamos visitado
dfs(u, v); // visitamos el hijo
if (disc[v] < low[u]) // comprobamos la condicion
bridges.push_back(pair<int,int>({u,v}));
low[v] = min(low[v], low[u]); // actualizamos low[v] para reflejar los backedges del subarbol
}
else { // nos encontramos con un backedge y actualizamos low[v] acordemente
low[v] = min(low[v], disc[u]);
}
}
}
void bridges() {
low = disc = vector<int>(G.size(), 0);
bridges = vector<pair<int,int>>();
nodos_visitados = 0;
// iteramos por si el grafo por si no es conexo visitarlo todo
for (int u = 0; u < adj.size(); u++)
if (!disc[u])
ap[u] = dfsAP(u, u) > 1; // condicion 1
}


Añadir nuevo comentario