Introducción
En geometría trabajamos con vectores y nos referimos a los números como escalares. Temas que se ven en las matemáticas de los últimos cursos de la ESO y primero de Bachillerato son útiles, como las identidades trigonométricas:
$$\sin^2(\alpha) + \cos^2(\alpha) = 1$$
$$\sin(\alpha + \beta) = \sin(\alpha)\cos(\beta) + \cos(\alpha)\sin(\beta)$$
$$\cos(\alpha + \beta) = \cos(\alpha)\cos(\beta) - \sin(\alpha)\sin(\beta)$$
$$\sin(-\alpha) = -\sin(\alpha), \ \cos(-\alpha) = \cos(\alpha), \ \sin(\alpha) = \cos(\pi / 2 - \alpha)$$
También es útil a veces el uso de coordenadas polares: si tenemos un punto $(x, y)$ y su distancia al origen $L = \sqrt{x^2+y^2}$, tenemos entonces que $(x, y) = (L \cos (\alpha), L \sin (\alpha))$, donde $\alpha$ será el ángulo del triangulo formado con el eje de coordenadas horizontal desde el origen.
Vectores
En este manual vamos a trabajar con vectores. Identificaremos los puntos con el vector del origen a ese punto, sin hacer distinción entre puntos y vectores en nuestra implementación. Toda la geometría que vamos a hacer es en 2D, por lo que un vector $u$ será una tupla $(u_1, u_2)$ de escalares.
Cuando todos los datos de entrada sean enteros, trataremos de hacer geometría usando únicamente valores enteros. Cuando esto no sea posible usaremos doubles, pero introducirá problemas de precisión.
using num = long long; // long double (si necesitas decimales y no puedes evitarlo)
struct Vec {
num x, y;
Vec() {}
Vec(num x_, num y_) : x(x_), y(y_) {} // define Vec(a, b) en el código
};
Podemos sumar y restar vectores componente a componente.
Si tenemos dos puntos $p = (p_x, p_y)$ y $q = (q_x, q_y)$ definimos el vector que va de $p$ a $q$ como $pq = q-p = (q_x-p_x, q_y-p_y)$.
Vec operator+(Vec u, Vec v) { // define u+v en el código
return Vec(u.x + v.x, u.y + v.y);
}
Vec operator-(Vec u, Vec v) { // define u-v en el código
return Vec(u.x - v.x, u.y - v.y);
}
Multiplicar un vector por un escalar $k$ lo definimos como multiplicar sus componentes: $k(u_1, u_2) = (k u_1, k u_2)$.
Vec operator*(num k, Vec u) { // define k*u en el código
return Vec(k * u.x, k * u.y);
}
Producto escalar y vectorial
Si tenemos dos vectores $u = (u_1, u_2), v = (v_1, v_2)$ su producto escalar es $u \cdot v = u_1 v_1 + u_2 v_2$, y su producto vectorial es $u \times v = \begin{vmatrix}
u_1 & v_1 \\
u_2 & v_2
\end{vmatrix} = u_1 v_2 - u_2 v_1$. Nota: el producto vectorial en 3D se define como un vector, que es perpendicular a los dos vectores $u$ y $v$, pero como trabajamos en 2D podemos identificar el producto vectorial con la componente Z del producto vectorial de $u$ y $v$ como vectores 3D contenidos dentro del plano XY.
num dot(Vec u, Vec v) {
return u.x * v.x + u.y * v.y;
}
num cross(Vec u, Vec v) {
return u.x * v.y - u.y * v.x;
}
A partir de ahora, inspirado por los símbolos con los que los expresamos, los llamaremos por sus nombres en inglés, dot product y cross product respectivamente.
La longitud o norma de un vector es $|u| = \sqrt{u_1^2 + u_2^2}$
num norm2(Vec u) { // norma al cuadrado
return dot(u,u);
}
num norm(Vec u) { // norma. Nota: Necesita decimales
return sqrt(norm2(u));
}
Ángulo entre dos vectores
¿Cómo podemos conocer el ángulo entre dos vectores? Tenemos las siguientes igualdades:
$$
u \cdot v = u_1 v_1 + u_2 v_2 = |u||v| \cos (\gamma) \\
u \times v = u_1 v_2 - u_2 v_1 = |u||v| \sin (\gamma)
$$
Podemos demostrar estas igualdades expresando $u$ y $v$ en forma polar, tenemos entonces que:
$$
u_1 = |u| \cos (\alpha), \hspace{1em} u_2 = |u| \sin (\alpha) \\
v_1 = |v| \cos (\beta), \hspace{1em} v_2 = |v| \sin (\beta)
$$
Si calculamos el dot product tenemos que $u \cdot v = |u||v|(\cos (\alpha) \cos (\beta) + \sin (\alpha) \sin (\beta)) = |u||v|\cos(\beta-\alpha) = |u||v|\cos(\gamma)$. Para el cross product se demuestra de manera similar.
Por tanto, podemos calcular el ángulo con funciones trigonométricas inversas. Pero, de hecho, normalmente no nos será necesario calcular el ángulo, sólo comparar ángulos.
En matemáticas usamos la convención de que un ángulo positivo es antihorario y un ángulo negativo es horario. Viendo que el signo de $u \times v$ será el signo de $\sin(\gamma)$, que a su vez es el signo de $\gamma$, ya tenemos una forma de ver en qué dirección tienes que girar si del vector $u$ quieres ir al vector $v$.
int sgn(num k) { // signo de un número
if (k > 0) return +1;
if (k < 0) return -1;
return 0;
}
const int IZQ = +1, DER = -1;
int orient(Vec u, Vec v) { // orientación = signo ángulo entre vectores
return sgn(cross(u, v));
}
Por ejemplo, supongamos que tenemos tres puntos $A,B,P$ en la siguiente disposición:
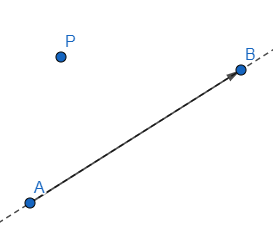
Decidimos la orientación $A \rightarrow B$, entonces el punto $P$ quedaría a la izquierda. Para poder encontrar la orientación de $P$ respecto a $A \rightarrow B$ definimos los vectores $u = B-A$ y $v = P-A$. Podemos calcular entonces $\texttt{orient(u, v)}$ que nos devolverá $-1$ ($\texttt{IZQ}$).
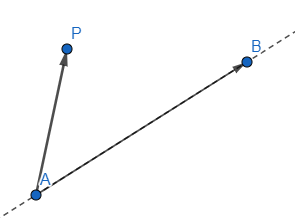
Ejercicio: ¿Se te ocurre cómo podrías usar esto para averiguar si dos segmentos intersecan?
Con estas operaciones básicas ya podemos resolver problemas bastante más complicados, por ejemplo, dado un polígono cualquiera, ¿cómo sabemos si un punto está dentro o fuera? Resulta que podemos inventarnos un segmento infinito (en la práctica muy muy largo, lo suficiente para que no acabe dentro del polígono) y contar cuántas veces pasa por el lado de un polígono, ya que cada vez que toca un lado sale o entra de este, alternando. La gracia de elegir un segmento infinito es que seguro que el extremo final está fuera, pero el inicial puede estar dentro o fuera, y la paridad del número de intersecciones nos dirá en qué caso estamos. Fíjate que los de dentro cruzan un número impar de veces los lados, y los de fuera un número par de veces:
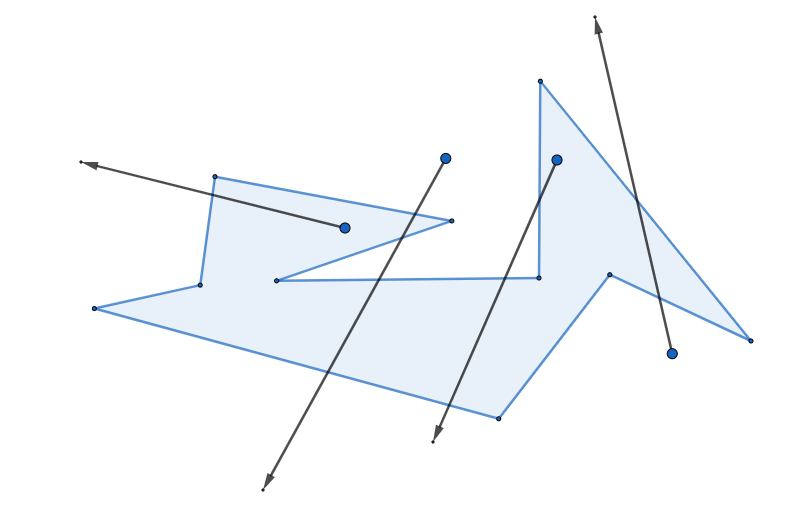
Si queremos saber dados $k$ puntos cuáles están dentro de un polígono de $n$ lados, este método tiene coste $\mathcal{O}(kn)$. Veremos más adelante que cuando es tengamos un polígono convexo podremos hacerlo en $\mathcal{O}(k \log n)$
Área de un polígono
Para determinar el area de un polígono simple (que no tenga intersecciones consigo mismo) como el anterior si tenemos los $n$ vértices ordenados consecutivamente $P_0,P_1,\dots,P_{n-1}$ podemos utilizar la fórmula del área de Gauss (o Shoelace Formula). Considerando $P_n = P_0$:
$$A = \frac{1}{2} \Bigg | \sum\limits_{i=0}^{n-1} P_i \times P_{i+1} \Bigg | = \frac{1}{2} \Bigg | \sum\limits_{i=0}^{n-1} x_i y_{i+1} - y_{i} x_{i+1} \Bigg |$$
En menos de diez minutos el siguiente video muestra con unas animaciones muy buenas por qué esto funciona: https://www.youtube.com/watch?v=0KjG8Pg6LGk
Polígonos convexos
Un polígono es convexo si toda línea entre dos de sus puntos queda completamente contenida dentro del polígono. Dicho de forma simple, que no tiene picos hacia dentro. Un ejemplo de polígono convexo (izquierda) y otro no convexo (derecha) con líneas entre punto (observad que en el no convexo hay líneas entre puntos que salen fuera):
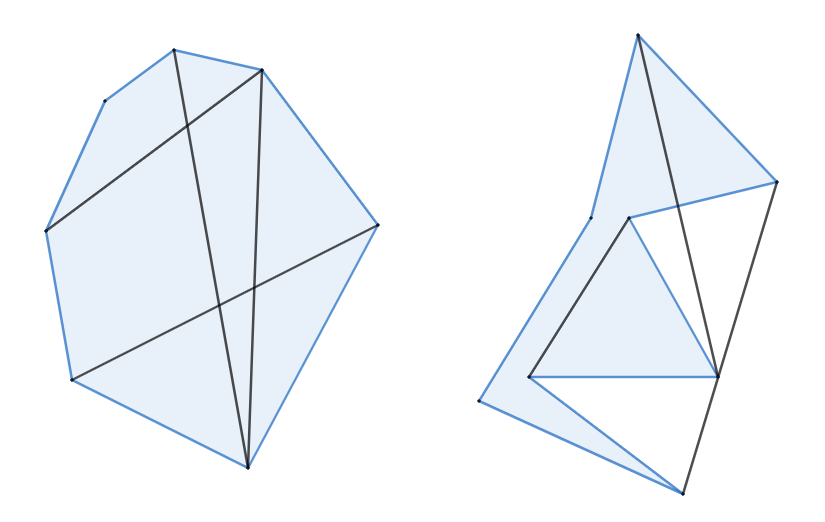
Vamos a retomar el problema de: dados $k$ puntos, determinar cuáles están dentro de un polígono, esta vez con un polígono convexo.
En un polígono convexo es muy fácil encontrar una triangulación, simplemente elegimos el punto inicial y cogemos los triángulos $(P_0, P_i, P_{i+1})$. Todo polígono simple admite triangulación, pero en el caso de los polígonos convexos es muy sencilla de encontrar.
Lo hacemos por ejemplo con el polígono convexo anterior:
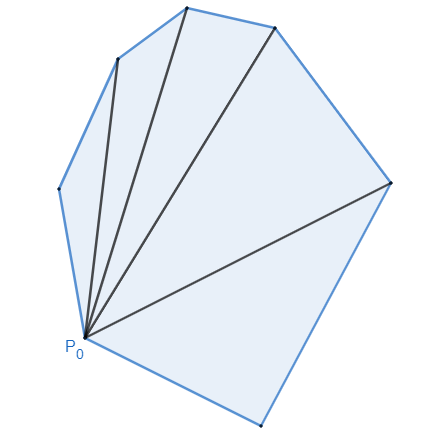
Si nos dan una lista de $k$ puntos, podemos ver los segmentos de la triangulación como vectores y los usaremos para resolver el problema de forma eficiente:
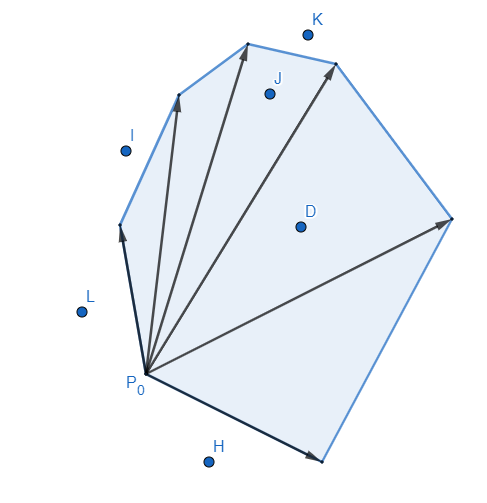
Primero encontraremos a qué triángulo le corresponde el punto, esto podemos hacerlo con una búsqueda binaria ya que, si el punto está dentro, separa los vectores en los que lo tienen a la derecha y los que lo tienen a la izquierda. Una vez tenemos los lados que deberían contener el punto (dos vectores consecutivos, uno que lo tiene a la derecha y otro a la izquierda) debemos asegurarnos que no se sale fuera del triángulo ya que por ejemplo el punto $K$ de la imagen también está entre los mismos dos vectores que el punto $J$ según este método. Para ver si el punto está dentro del triángulo, consideramos el segmento entre los extremos de los dos vectores y (cuando decidamos una orientación) miramos si el punto queda hacia el lado de dentro o hacia el lado de fuera.
Envolvente convexa
La envolvente convexa de un conjunto de puntos (convex hull) es el polígono convexo mínimo que cubre todos los puntos dados. Una forma intuitiva de imaginarlo es como si tuviéramos unos clavos en una pared y pusiéramos una cuerda alrededor de todos ellos tensada, o una goma elástica.
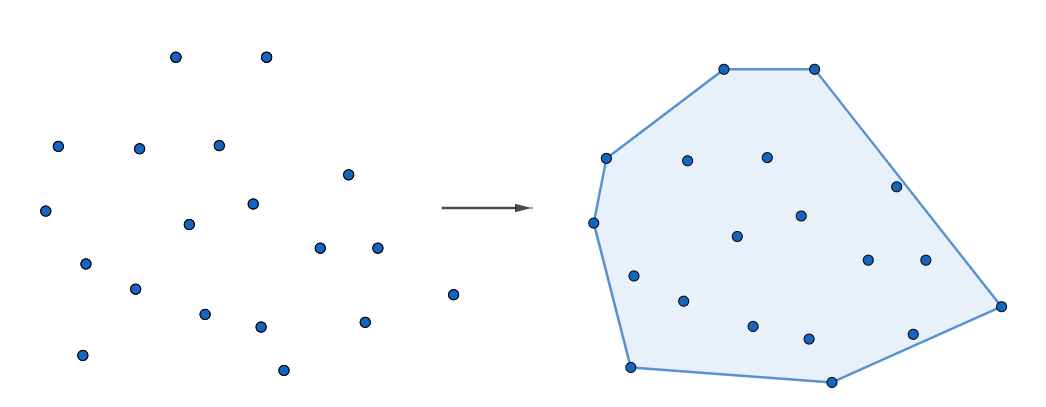
Es una de las cosas más útiles en geometría computacional, así que empezaremos por lo importante: ¿cómo se calcula eficientemente?
El método de Graham (Graham's scan) nos permite calcular el convex hull de $n$ puntos en $\mathcal{O}(n \log n)$, y si nos dieran los puntos ordenados convenientemente solo necesitaría $\mathcal{O}(n)$.
En primer lugar debemos ordenar los puntos angularmente. ¿Qué significa esto? Vamos a definir un punto origen conveniente, en este caso diremos que $P_0$ es el punto más abajo a la izquierda, es decir, el punto con mínima coordenada $y$ y en caso de empate el que tenga mínima coordenada $x$.
Vec p0 = P[0];
for (Vec p : P)
if (p.y < p0.y or (p.y == p0.y and p.x < p0.x)) p0 = p;
Ahora ordenaremos el resto de puntos $P_i$ por el ángulo que forma el vector de $P_0$ a $P_i$ con la horizontal.
Para hacer esto no es necesario calcular ángulos. Vamos a definir una función $\texttt{orient(A, B, C)}$ que dados tres puntos, nos diga si el punto $C$ queda a la izquierda respecto al segmento $A \rightarrow B$ o a la derecha. Con esto ya podremos comparar fácilmente qué punto va antes o después, mirando si uno está a la izquieda del otro o a la derecha. En caso de que estén alineados, queremos primero el que esté más cerca, es decir, el que tenga el vector más corto desde $P_0$:
int orient(Vec a, Vec b, Vec c) {
return orient(b-a, c-a);
}
bool left(Vec a, Vec b, Vec c) {
return orient(a, b, c) == IZQ;
}
bool right(Vec a, Vec b, Vec c) {
return orient(a, b, c) == DER;
}
... // después de encontrar p0:
sort(P.begin(), P.end(), [&p0](Vec a, Vec b) {
if (left(p0, a, b)) return true;
if (right(p0, a, b)) return false;
return norm2(a-p0) < norm2(b-p0);
});
Una vez ordenados, usaremos una stack para mantener el convex hull hasta haber procesado todos los puntos en $\mathcal{O}(n)$. La idea es que si miramos los puntos en orden angular, los que están en el convex hull siempre son un giro en la misma dirección, en este caso siempre hacia la izquierda, y queremos ir borrando los que provocan una esquina hacia dentro, que serán los que causen un giro hacia la derecha (o estén alineados).
vector<Vec> ch; // aquí vamos guardando el convex hull
for (Vec p : P) {
while (ch.size() >= 2 and not left(ch[ch.size()-2], ch.back(), p)) {
ch.pop_back();
}
ch.push_back(p);
}
Es fácil ver que el tiempo de esta parte es lineal ya que cada punto solo puede entrar al stack una vez, y por tanto solo puede salir una vez. Cada paso de los bucles añade o quita un punto por lo que en total hace como mucho $\sim2n$ pasos.
En la entrada de Wikipedia del método de Graham hay animaciones que ilustran el proceso.
Ejercicio: Dados $n$ puntos, ¿sabrías encontrar la pareja con mayor distancia entre ellos en $\mathcal{O}(n \log n)$?
Convex hull con o sin puntos alineados
Dependiendo del problema queremos o no que los puntos alineados se consideren del convex hull o solo los de los extremos. Hay que hacer algunas modificaciones al código para adaptarlo al caso de las alineaciones, al final del documento está el código completo, que es largo ya que tiene todas las funciones explicadas implementadas. En la práctica, no siempre hace falta definir todo y puede programarse mucho más corto, pero si vamos a hacer problemas complicados merece la pena tener todas estas operaciones definidas.
Cabe mencionar que hay un problema cuando aceptamos alineaciones, los posibles puntos alineados de la última recta al dar la vuelta tienen que ordenarse de lejano a cercano, al revés de como los tenemos, lo que también está considerado en el código mencionado.
Algunas fórmulas
Fórmula de Herón
Si tenemos un triángulo cualquiera de lados $a, b, c$, podemos calcular su area con la fórmula de Herón.
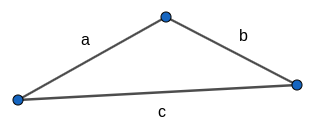
Definimos el semiperímetro $s = \frac{\text{perímetro}}{2} = \frac{a+b+c}{2}$ y entonces tenemos que el área es $A = \sqrt{s(s-a)(s-b)(s-c)}$
Teorema de Pick
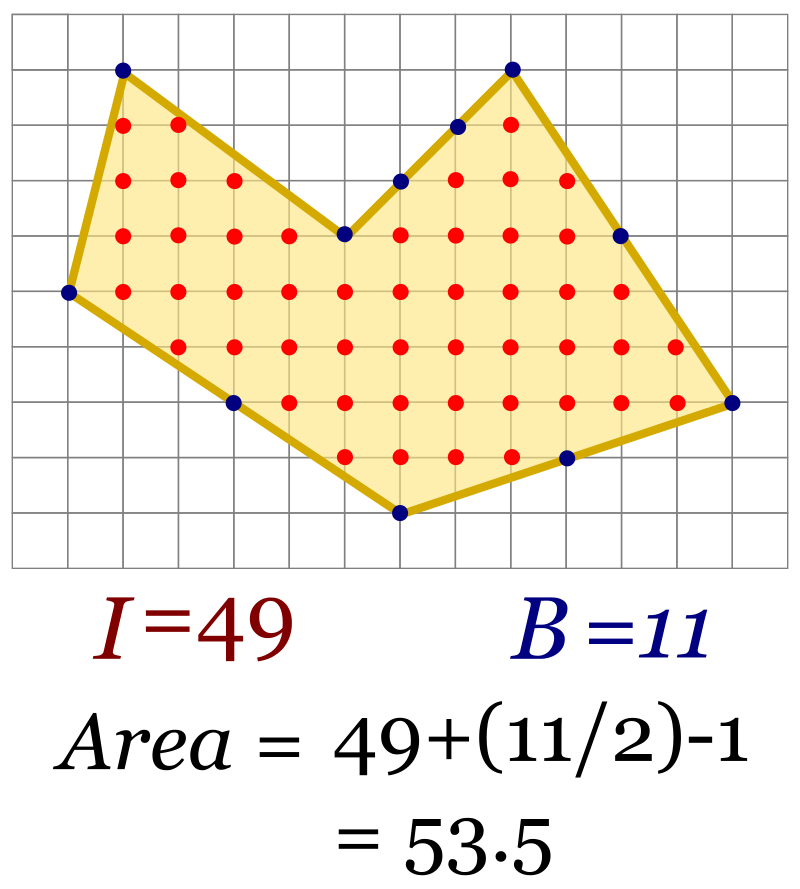
Si tenemos un triángulo con vértices con coordenadas enteras, el teorema de Pick nos dice lo siguiente: Si tenemos $B$ puntos enteros en los bordes e $I$ puntos enteros en el interior, el área será:
$$A = I + \frac{B}{2} - 1$$
Más geometría
En este manual no podemos cubrir más geometría, y a nivel preuniversitario muy raramente vais a necesitar conocer algoritmos más complejos de geometría. Si os interesa y queréis aprender más sobre este tema, recomendamos los siguientes recursos:
Handbook of geometry for competitive programmers: https://victorlecomte.com/cp-geo.pdf
Algorithms for Competitive Programming (apartado geometría): https://cp-algorithms.com/geometry/basic-geometry.html
Código Convex Hull Completo
// Código Convex Hull completo, con/sin alineaciones
#include <bits/stdc++.h>
using namespace std;
using num = long long; // long double (si necesitas decimales y no puedes evitarlo)
struct Vec {
num x, y;
Vec() {}
Vec(num x_, num y_) : x(x_), y(y_) {} // define Vec(a, b) en el código
};
Vec operator+(Vec u, Vec v) { // define u+v en el código
return Vec(u.x + v.x, u.y + v.y);
}
Vec operator-(Vec u, Vec v) { // define u-v en el código
return Vec(u.x - v.x, u.y - v.y);
}
Vec operator*(num k, Vec u) { // define k*u en el código
return Vec(k * u.x, k * u.y);
}
num norm2(Vec u) { // norma al cuadrado
return u.x*u.x + u.y*u.y;
}
num dot(Vec u, Vec v) {
return u.x * v.x + u.y * v.y;
}
num cross(Vec u, Vec v) {
return u.x * v.y - u.y * v.x;
}
int sgn(num k) { // signo de un número
if (k > 0) return +1;
if (k < 0) return -1;
return 0;
}
const int IZQ = +1, DER = -1;
int orient(Vec u, Vec v) { // orientación = signo angulo entre vectores
return sgn(cross(u, v));
}
int orient(Vec a, Vec b, Vec c) {
return orient(b-a, c-a);
}
bool left(Vec a, Vec b, Vec c, bool consider_align=false) {
int o = orient(a, b, c);
return o == IZQ or (consider_align and o == 0);
}
bool right(Vec a, Vec b, Vec c, bool consider_align=false) {
int o = orient(a, b, c);
return o == DER or (consider_align and o == 0);
}
int main() {
int n;
cin >> n;
vector<Vec> P(n);
for (int i = 0; i < n; ++i) cin >> P[i].x >> P[i].y;
const bool include_collinear = true;
Vec p0 = P[0];
for (Vec p : P) {
if (p.y < p0.y or (p.y == p0.y and p.x < p0.x))
p0 = p;
}
sort(P.begin(), P.end(), [&p0](Vec a, Vec b) {
if (left(p0, a, b)) return true;
if (right(p0, a, b)) return false;
return norm2(a-p0) < norm2(b-p0);
});
if (include_collinear) {
int i = n-1;
while (i-1 >= 0 and orient(p0, P[i], P[i-1]) == 0) {
--i;
}
reverse(P.begin()+i, P.begin()+n);
}
vector<Vec> ch;
for (Vec p : P) {
while (ch.size() >= 2 and right(ch[ch.size()-2], ch.back(), p, not include_collinear)) {
ch.pop_back();
}
ch.push_back(p);
}
cout << ch.size() << endl;
for (Vec p : ch) {
cout << p.x << " " << p.y << endl;
}
}


Añadir nuevo comentario