Los problemas de programación dinámica se pueden pensar en términos de estados y transiciones: los estados son los resultados a los subproblemas que se almacenan, y las transiciones son las funciones que se utilizan para calcular los valores de unos estados en función de las anteriores o bien de forma recursiva (en dinámicas top-down) o bien de forma iterativa.
Aquí se muestran algunos ejemplos de clasificatorios de la OIE resueltos:
Ejemplo 1: (Clasificatorio OIE 2018)
Una montaña rusa de longitud $L$ es una atracción que consta de $2L$ tramos, puestos uno detrás del otro. Solamente existen dos tipos de tramos: los ascendentes y los descendentes. Cada tramo mide exactamente una unidad de longitud en su componente horizontal y una unidad de longitud en su componente vertical. Es decir, que cada tramo avanza una unidad de longitud ascendente o descendente y una unidad de longitud horizontalmente, en función de si es un tramo ascendente o descendente. Además, las montañas rusas no tienen ningún tramo bajo tierra, y empiezan y acaban al nivel del suelo.
La altura de una montaña rusa es la distancia sobre el nivel del suelo de su punto más alto. Se pide calcular el número de montañas rusas de longitud $L$ y altura $H$ \((1 \leq L, H \leq 200)\). El programa recibe $T$ \((T \leq 4\cdot10^4)\) pares de enteros $L, H$ y se debe imprimir la solución para cada uno de ellos módulo $10^9+7$.
Solución:
A primera vista, localizamos dos parámetros de interés: la longitud de una montaña rusa y su altura. Sin embargo, si se piensa sólo en términos de estos dos parámetros, no podemos encontrar una relación de recurrencia directa: no parece haber ninguna relación obvia entre el número de montañas rusas de longitud $L$ y longitud $L-1$, o las de altura $H$ y $H-1$. Vamos a pensar en qué necesitamos para encontrar una relación de recurrencia: el último tramo tiene que ser necesariamente descendente, así que el número de montañas rusas de longitud $L$ y altura $H$ es el mismo que el número de “pseudomontañas” con $2L-1$ tramos y altura $H$ que acaban a una altura de $1$. El penúltimo tramo puede o ser bien ascendente, en cuyo caso está precedido por una montaña rusa de longitud $L-1$ y altura $H$ y tenemos una relación de recurrencia, o bien descendente (si la altura máxima es mayor o igual a $2$), y entonces tenemos otra vez una “pseudomontaña” que acaba en una altura de $2$.
Esto nos da una idea: si consideramos la variable “altura en la que acaba la montaña”, tenemos una relación de recurrencia sencilla. Así, definiríamos el “estado” del problema con 3 variables: sea f(t, ch, mh) el número de montañas con t tramos que acaban en una altura ch y llegan a una altura máxima mh. Entonces lo que buscamos es f(2*L, 0, H). Las transiciones son las siguientes:
f(t, 0, mh) = f(t-1, 1, mh) , porque cuando se está a altura 0 el tramo anterior tiene que ser necesariamente descendente.
f(t, ch, mh) = f(t-1, ch-1, mh) + f(t-1, ch+1, mh) si 0 < ch < mh, porque para cualquier altura positiva menor que la máxima el tramo anterior puede ser tanto descendente como ascendente.
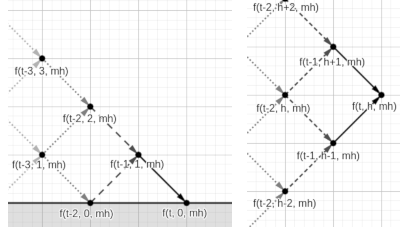
f(t, mh, mh) = f(t-1, mh-1, mh) + f(t-1, mh-1, mh-1). Esta recurrencia es un poco más complicada: si la altura a la que acaba la montaña es igual a su altura máxima, entonces claramente el tramo anterior es ascendente, pero hay dos casos: o bien la montaña formada sin el último tramo tiene otro pico con la altura máxima, entonces la altura máxima sigue siendo la misma, o el último tramo era cuando la montaña alcanzaba la altura máxima, en ese caso la montaña sin el último tramo tiene una altura máxima una unidad inferior.
Tenemos como casos base de la recurrencia f(0, 0, 0) = 1 y f(0, x, y) = 0 para cualquiera otros valores (x, y), porque no queremos contar montañas que empiecen sobre una altura superior a 0 y para que el parámetro de altura máxima tenga coherencia. Almacenamos el resto de dividir f(t, ch, mh) por $10^9+7$ en un vector tridimensional de $401 \times 201 \times 201$: nótese que, por muchas solicitudes de pares $(L, H)$ que reciba el programa, la cantidad de cálculos que se hacen está acotada porque reutilizamos los estados calculados en solicitudes anteriores.
Aquí se puede encontrar una solución implementada de forma top-down. Este problema también se podría haber pensado de forma bottom-up: entonces, en lugar de pensar en “cuál puede haber sido el tramo anterior” para obtener una relación recursiva, pensaríamos en “cuál puede ser el tramo siguiente” para obtener una relación iterativa. En este caso, las “transiciones” son un poco más sencillas, en particular el caso en el que cambia la altura máxima: sólo puede aumentar la altura máxima con el tramo siguiente si actualmente estás en la altura máxima de la montaña y el tramo siguiente es ascendente.
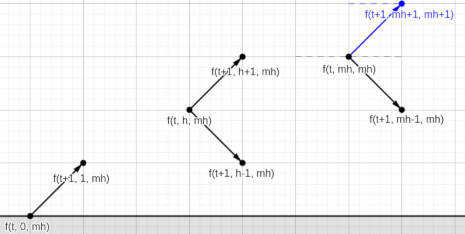
Una observación que podemos hacer es que, para el cálculo de la respuesta para un par $(L, H)$ concreto, el planteamiento bottom-up permite ahorrarnos memoria porque f(t+1, ch, mh) depende sólo de f(t, ch, mh): así podemos eliminar una de las dimensiones del vector. Sin embargo, como nos piden muchos pares $(L, H)$, es conveniente almacenar todos los estados para poder reutilizarlos.
Ejemplo 2: (Clasificatorio OIE 2019)
Se da un texto (de longitud $\leq 1000$ caracteres). Se quiere escribir el texto utilizando el siguiente teclado (los espacios en blanco del texto se ignoran):

Quien escribe el texto empieza a escribir teniendo su dedo índice izquierdo sobre la tecla F y su dedo índice derecho sobre la tecla J. En cualquier momento, puede desplazar cualquiera de sus dedos a una de las cuatro teclas adyacentes (o tres o dos si se encuentra en un borde del teclado) y tarda un segundo en hacer este movimiento. Además, es capaz de desplazar ambos dedos simultáneamente. Puede pulsar una tecla instantáneamente (es decir, en cero segundos) si tiene uno de sus dos índices sobre ella. Tiene unos brazos infinitamente flexibles, es decir, que puede entrelazarlos sin problema alguno. Encontrar el mínimo tiempo necesario para escribir el texto.
Solución:
En este problema, el estado viene dado por los tres parámetros (número de caracteres que se han escrito, posición del dedo derecho, posición del dedo izquierdo). Las transiciones entre estados se hacen así: el tiempo mínimo necesario para escribir hasta el caracter n con los dedos en una determinada posición es el mínimo entre [ los tiempos necesarios para escribir hasta el caracter n-1, con uno de los dedos en la posición de la tecla correspondiente y el otro en cualquier otra posición y sumando la distancia máxima entre las posiciones actuales de los dedos y las posiciones anteriores ].
Conceptualmente, este problema es sencillo (ver cuál es el estado no es complicado y las transiciones son bastante naturales), pero la dificultad radica en implementarlo de forma rápida y correcta. Recomendamos a los lectores intentarlo: es una buena práctica de programación, especialmente para aquellos que no tienen demasiada soltura escribiendo programas más complicados. Aquí está la implementación oficial, que aprovecha la clase map de la STL de C++ para describir la posición espacial de las teclas sin escribir mucho código. Merece la pena mirarla, porque algunas cosas se hacen de forma un poco distinta a lo que se ha explicado aquí: en concreto, la función f(a, b, c, d, e), con a siendo el número del carácter, (b, c) es la posición del dedo izquierdo y (d, e) la del derecho no retorna el mínimo tiempo hasta el carácter a, sino el mínimo tiempo desde el carácter a, cosa que simplifica la implementación al poder codificar la posición inicial de los dedos de forma más sencilla. Además, incluye una pequeña optimización: en lugar de considerar todas las posiciones posibles del segundo dedo (el que no se mueve a la tecla que hay que pulsar, queremos decir) sólo considera las que no van más lejos del movimiento del primer dedo. Dejamos a los lectores pensar por qué esta optimización puede hacerse.


Añadir nuevo comentario