Estructura Unión-Búsqueda en conjuntos disjuntos (I): Introducción

Queremos diseñar una estructura de datos, que dados unos elementos, se puedan clasificar en conjuntos (disjuntos) de forma que las siguientes operaciones se ejecuten rápidamente:

• Dado un elemento, determinar a qué conjunto pertenece. (En particular, estaremos interesados en saber cuándo dos elementos pertenecen al mismo conjunto)
• Dados dos conjuntos, unirlos, es decir, hacer que los elementos de los dos conjuntos pasen a estar en un solo conjunto.

Puede ser un poco difícil entender qué utilidad podría tener esta estructura de datos. Como ilustración de una aplicación pondremos el Algoritmo de Kruskal. Podéis leer el manual correspondiente para conocer más detalles: aquí sólo damos el esquema del algoritmo.

Dado un grafo $G$ y otro grafo $T$ con los mismos vértices que $G$ pero inicialmente sin aristas, el algoritmo itera por las aristas del grafo $G$ ordenadas de menor a mayor peso y, si la arista actual al añadirse a $T$ no genera un ciclo, se añade a $T$.  En pseudocódigo:

sort(EdgeListG)
for (u, v) in EdgeList(G)
    if ((u, v) does not create cycle in T)
        add (u, v) to T

La parte “complicada” del algoritmo es comprobar si al añadir cada arista se forma un ciclo. Podríamos, por ejemplo, añadir la arista, comprobar si hay un ciclo en el grafo $T$ explorándolo con un DFS o un BFS y borrarla si encontramos un ciclo. Pero eso no sería eficiente, porque entonces en cada comprobación utilizamos un tiempo proporcional a $\mathcal{O}(V)$. La observación que tenemos que hacer es que “\((u, v)\) hace que se forme un ciclo en $T$ (que antes era acíclico)” es equivalente a “$u$ y $v$ están en la misma componente conexa de $T$”, y además, cuando se añade la arista $(u, v)$ se produce una unión de las componentes conexas correspondientes a los vértices $u$ y $v$. Es aquí donde entra en juego nuestra estructura de datos: si al principio cada vértice está en un conjunto separado, para cada arista $(u, v)$ comprobamos si $u$ y $v$ están en el mismo conjunto, y si no lo están añadimos la arista y unimos los dos conjuntos en los que están $u$ y $v$. Es decir, nuestra colección de conjuntos lo que hace es mantener la colección de componentes conexas de $T$ mientras vamos añadiendo aristas.

Ahora que ya hemos explicado una aplicación, vamos a ver cómo implementar esta estructura. La idea principal es que los conjuntos no serán definidos “explícitamente”, sino “implícitamente”, a través de un elemento representativo de cada conjunto. Para encontrar cuál es el conjunto al que pertenece cada elemento, cada elemento tiene asociada una referencia a otro elemento. Si el elemento se tiene a sí mismo como referencia, esto significa que ese elemento es el elemento representativo de su propio conjunto. Si el elemento tiene a otro elemento como referencia, ese otro elemento puede ser el elemento representativo del conjunto o puede tener otro elemento distinto como referencia, pero de tal forma que siguiendo esta cadena de referencias se llegue finalmente a un elemento que se tenga a sí mismo como referencia, que será el elemento representativo del conjunto al que pertenece el elemento inicial. De esta forma, para unir los conjuntos correspondientes a $u$ y $v$, sólo hay que asignar la referencia del elemento representativo del conjunto correspondiente a $u$ al elemento representativo del conjunto de $v$. Vamos a poner un ejemplo para que se entienda mejor:

Tenemos inicialmente $6$ elementos, tales que cada uno está contenido en un conjunto. Digamos que queremos unir el conjunto del $2$ con el conjunto del $1$ y el conjunto del $4$ con el conjunto del $3$. Es muy sencillo: simplemente asignamos las referencias del $2$ y del $4$ al $1$ y el $3$, respectivamente.

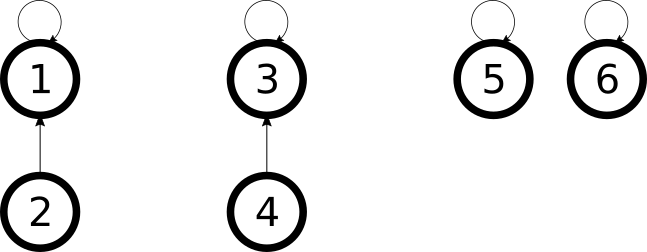
Ahora supongamos que queremos unir el conjunto donde está el elemento $4$ al conjunto donde está el elemento $1$. No es tan sencillo como cambiar la referencia del $4$ al $1$: tenemos que encontrar el elemento representativo del conjunto donde está el $4$ y luego cambiar la referencia al $1$ (que es el elemento representativo de su conjunto).

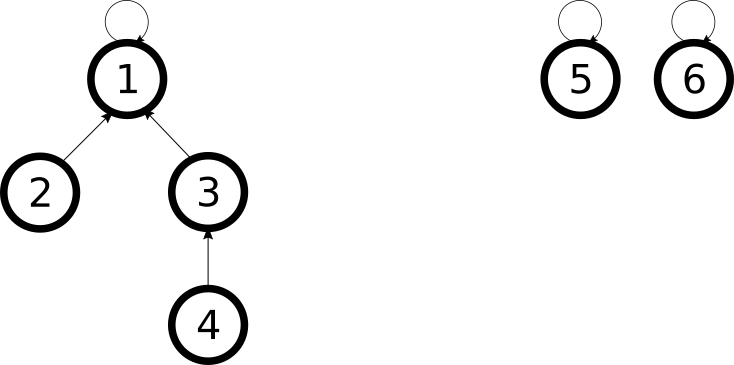
Para comprobar si dos elementos están en el mismo conjunto, encontramos los elementos representativos del conjunto de cada elemento y vemos si son iguales. Para encontrar el elemento representativo de un conjunto seguimos la cadena de referencias hasta que encontramos el elemento que se referencia a sí mismo. En esta imagen vemos que los conjuntos forman árboles cuya raíz es el elemento representativo, y cada referencia indica cuál es el padre del elemento.

Por último, si queremos unir los conjuntos del $4$ y el $6$, acaba saliendo esto:

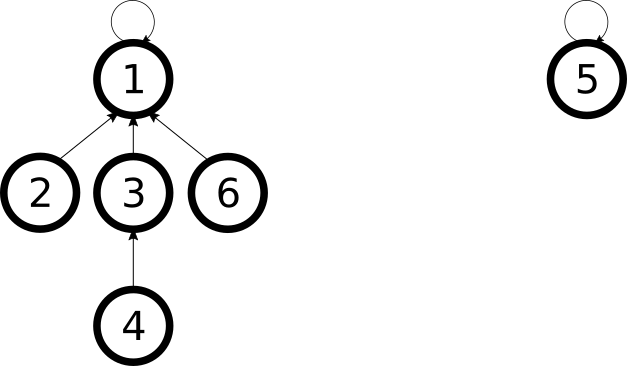
Es fácil ver que esta estructura de datos no es eficiente: se pueden formar cadenas bastante largas, haciendo que el tiempo de las operaciones de búsqueda y unión sea lineal en el número de elementos. Sin embargo, la idea básica de la estructura es esta: haciendo sólo unas pequeñas modificaciones que veremos en el siguiente manual, conseguiremos unas mejoras considerables, haciendo que las operaciones tarden un tiempo casi \(\mathcal{O}(1)\). Pero antes, presentamos una posible implementación en C++ de lo que ya tenemos.

vector<int> p; //p[i] = referencia del i-ésimo elemento. Inicialmente, p[i] = i;

//retorna el elemento representativo del conjunto en el que está el i-ésimo elemento
int findSet(int i) {
    if(p[i] == i) return i;
    return findSet(p[i]);
}
//une los conjuntos correspondientes a los elementos u y v
void unionSet(int u, int v) {
    p[findSet(u)] = findSet(v);
}

Ejercicio 1: ¿Qué pasaría si pusiéramos p[findSet(u)] = v; en lugar de p[findSet(u)] = findSet(v); ? ¿Por qué lo hemos puesto de la segunda forma?
Ejercicio 2: ¿Cómo lo haríamos para poder consultar el número de elementos que tiene cada conjunto? (Esto lo usaremos en el siguiente manual)