Hay dos mejoras que se pueden hacer para hacer más eficiente la estructura de datos que planteamos en el manual anterior. Las dos mejoras se conocen como unión por tamaño (union by size) y compresión de caminos (path compression).
Veamos una situación en la que la estructura de Unión-Búsqueda es ineficiente: si tenemos inicialmente cada elemento en un conjunto y llamamos a unionSet(1, 2), unionSet(2, 3), unionSet(3, 4), ..., unionSet(m-1, m) acabamos teniendo una cadena de longitud $m$ y cada vez que llamemos a findSet(1) tendremos que atravesar los $m$ nodos. ¿Cómo podemos mejorar esta situación?
Unión por tamaño
Una observación que podemos hacer es que este inconveniente aparece porque vamos uniendo la larga cadena de nodos de forma que siempre se añade la cadena como hija de un nuevo nodo, nunca se crean ramificaciones. Si en lugar de hacer unionSet(1, 2), unionSet(2, 3), unionSet(3, 4) hiciéramos unionSet(2, 1), unionSet(3, 2), unionSet(4, 3), tendríamos todo lo contrario: en lugar de una larga cadena, tendríamos el elemento $1$ como elemento representativo y todos los demás elementos directamente conectados con él.
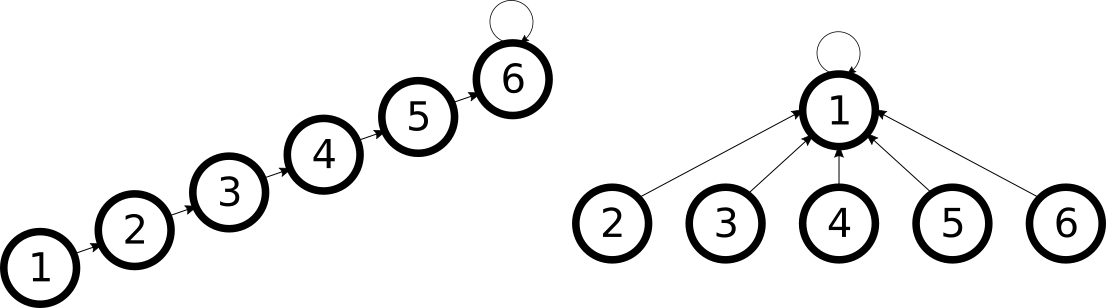
Los dos árboles representan el mismo conjunto, pero el de la derecha responde más eficientemente.
La idea importante es que no estamos obligados a unir los nodos en el orden tal como se nos da en los parámetros de la función: como da igual qué elemento sea el representativo, podemos tratar de hacerlo de la forma más conveniente. Un posible criterio para unir dos conjuntos que evita el problema de las cadenas largas es la unión por tamaño: ponemos como padre el elemento característico del conjunto de mayor tamaño (desempatando arbitrariamente). Se puede intuir que esto evitará que se formen cadenas muy largas, pero se puede establecer una cota formalmente:
Ejercicio 1: Para una estructura con n elementos, construir una sucesión de operaciones de unión (con el criterio de unión por tamaño) que de como resultado un árbol con un camino desde un nodo hasta la raíz de longitud \(\Omega(\log n)\)
Ejercicio 2: Demostrar que no pueden formarse caminos con longitud mayor a $\log n$.
Así, tenemos que utilizando este criterio para la unión, cada operación tiene un coste en el peor caso de $\mathcal{O}(\log n)$. Bastante mejor que el $\mathcal{O}(n)$ que teníamos sin utilizar esta heurística. Para implementar este criterio, almacenamos en un vector adicional el tamaño del subárbol que hay bajo cada elemento y lo actualizamos después de cada unión.
void unionSet(int u, int v) {
int ru = findSet(u);
int rv = findSet(v);
if(size[ru] < size[rv]) {
p[ru] = rv;
size[rv] += size[ru];
}
else {
p[rv] = ru;
size[ru] += size[rv];
}
}
Compresión de caminos
Olvidemos por un momento la mejora anterior y volvamos al problema que teníamos inicialmente: cadenas demasiado largas, cada vez que llamamos a findSet tenemos un coste $\mathcal{O}(n)$. Otra idea distinta para mejorar esto es que no tenemos que recorrer toda la cadena de nodos varias veces. Una vez hemos encontrado el elemento representativo de un conjunto, podemos hacer que todos los nodos por los que hemos pasado apunten directamente a ese elemento representativo para que las consultas posteriores sean más rápidas. Así, “comprimimos” los caminos después de recorrerlos.

Implementar esto es muy fácil tal como teníamos implementada la función findSet:
int findSet(int i) {
if(p[i] != i) p[i] = findSet(p[i]);
return p[i];
}
Nótese que con esta mejora el coste de una operación en el peor caso sigue siendo $\mathcal{O}(n)$, ya que seguimos pudiendo generar cadenas arbitrariamente largas, aunque después se compriman cuando las recorremos. Sin embargo, el coste amortizado de una operación, es decir, el coste promedio de las operaciones dentro de una secuencia de operaciones, es mucho menor. En el ejemplo de generar una cadena de $m$ nodos: en cada una de las $m-1$ uniones se visitan $\mathcal{O}(1)$ nodos, así que en total el coste de las uniones es $\mathcal{O}(m)$, y después hacer una operación findSet tiene un coste $\mathcal{O}(m)$, así que el coste total de las $m$ operaciones es $\mathcal{O}(m) + \mathcal{O}(m) = \mathcal{O}(m)$ y por tanto el coste promedio por operación es $\mathcal{O}(1)$. Es decir, como para construir la cadena se necesitan $m-1$ operaciones muy rápidas, aunque luego hagas una operación lenta (que si la repites deja de ser lenta porque se comprime el camino) el coste promedio de las operaciones sigue siendo bajo.
Ejercicio 3: Dada una estructura con $n$ elementos que use compresión de caminos pero no unión por tamaño, encontrar una secuencia de $m \leq n$ operaciones cuyo coste total sea \(\Omega(n \log n)\) (por tanto, teniendo un coste amortizado de \(\Omega(\log n)\) por operación)
Se puede demostrar que este es el peor caso, es decir, que el coste amortizado por operación en una estructura con compresión de caminos es $\mathcal{O}(\log n)$, pero es más complicado. De hecho, si el número de operaciones es mayor que $n$, la complejidad es mejor que logarítmica. Para más detalles ver (Tarjan, Van Leeuwen 1984).
Juntando ambas heurísticas
Utilizando o bien unión por tamaño o bien compresión de caminos conseguimos una complejidad (amortizada) de $\mathcal{O}(\log n)$ por operación. Esto está bastante bien (de hecho, ya nos sirve para aplicaciones como el algoritmo de Kruskal que comentábamos en el manual anterior, ya que este algoritmo ya tiene $\mathcal{O}(n \log n)$ de complejidad porque hace una ordenación), pero si juntamos las dos optimizaciones resulta que cada operación tiene coste amortizado $\mathcal{O}(\alpha(n))$, donde $\alpha(n)$ es la inversa de la función de Ackermann, que crece tan lentamente que puede considerarse constante a efectos prácticos.
Realmente, sólo es necesario implementar la heurística de compresión de caminos, ya que el factor constante adicional de implementar la heurística de unión por tamaño hace que en la práctica no se gane eficiencia implementando las dos heurísticas. Además, programar sólo la heurística de compresión de caminos es muy fácil, tal como hemos dicho antes. Pero esto no significa que la idea de la unión por tamaño sea inútil: esta heurística tiene otras aplicaciones a parte de esta estructura de datos y puede ayudar tenerla en mente al resolver algunos problemas.
Nota: una cosa que hay que tener en cuenta si se quiere implementar la estructura con las dos heurísticas es que ahora size[i] en general no contiene el tamaño de los subárboles de cada nodo, ya que no lo actualizamos al comprimir los caminos. No hace falta actualizarlo porque los valores para los elementos característicos, que es lo que nos importa para la heurística de unión por tamaño, sí son correctos.


Añadir nuevo comentario