Vocabulario Teoría de Grafos

Un grafo es un conjunto de vértices (o nodos) y un conjunto de aristas (o arcos) que los unen. Gráficamente, se suelen representar los vértices como puntos en el plano y las aristas como segmentos que los unen.

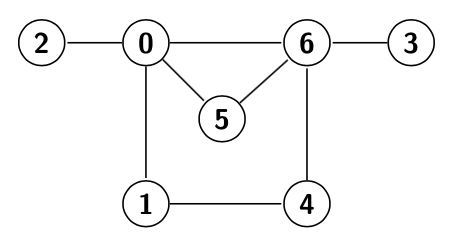
Conceptos de grafos

Veamos una serie de conceptos que se emplean frecuentemente en el campo de teoría de grafos:

Decimos que dos nodos están conectados si podemos ir de uno a otro a través de arcos:

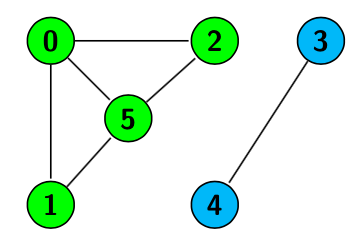
Por ejemplo, el nodo 1 y el nodo 2 están conectados, pero el nodo 5 y el 4 no. Si todos los nodos están conectados hablamos de grafo conexo. Decimos que todos los nodos que están conectados entre sí forman una componente conexa así pues los nodos verdes forman una componente conexa y los nodos azules forman otra componente conexa. 

Grado de un nodo: Es el número de aristas conectadas al nodo.

Grafo dirigido: Grafo en el que los arcos tienen sentido. Si los arcos no tienen sentido hablamos de un grafo no dirigido

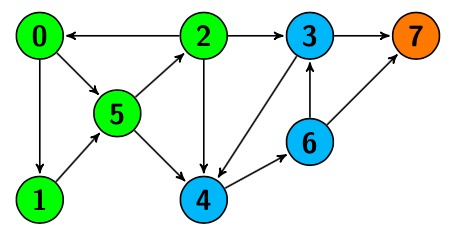
Por ejemplo, este grafo es dirigido, mientras que los anteriores no lo eran. En el contexto de grafos dirigidos, decimos que un conjunto de vértices forman una componente fuertemente conexa si es posible ir de un nodo cualquiera del conjunto a cualquier otro, en el ejemplo cada una de las componentes conexas tiene asignada un color.

Grafo ponderado (o con pesos): Grafo en el que las aristas tienen un peso asociado

Camino: Es un grafo en el que podemos nombrar a los nodos de modo que dos nodos están conectados si y solo si su diferencia es 1.

Ciclo: Es un conjunto de nodos donde cada uno está conectado al siguiente y el ultimo al primero

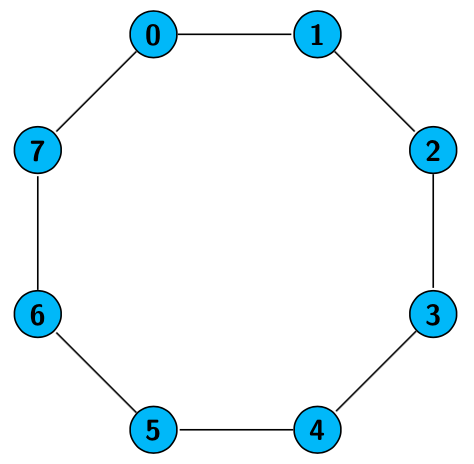
Grafo completo: Es un grafo en el que todo par de vértices están conectados.

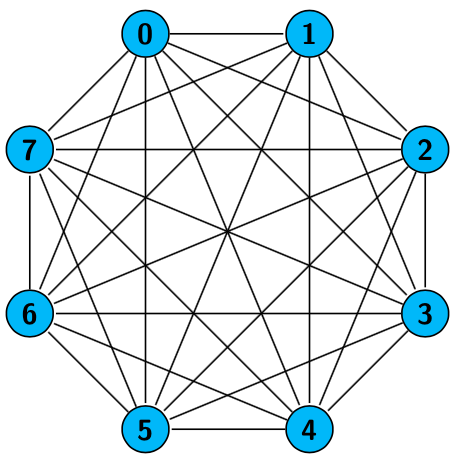
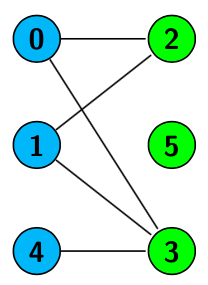
Grafo bipartido: Grafo en el que podemos agrupar los vértices en dos clases, de modo que no haya arcos entre los vértices de una misma clase.

Árbol: Grafo conexo y sin ciclos:

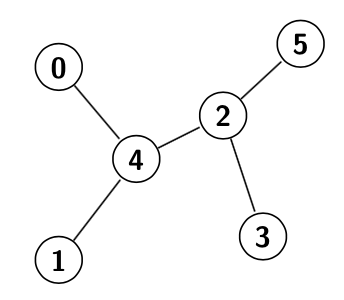
A un conjunto de árboles se le llama bosque. En determinadas ocasiones podemos considerar que el árbol tiene un nodo principal, en este caso hablamos de árbol arraigado, en este tipo de árboles a los nodos adyacentes más alejados de la raíz se les llama hijos, mientras que al nodo adyacente más cercano a la raíz se le llama padre, finalmente, a los nodos sin hijos se les llama hojas.

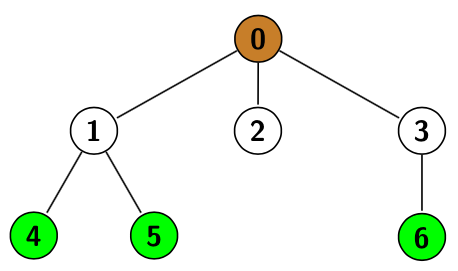
Por ejemplo, en este grafo, si consideramos que el nodo 0 es la raíz del árbol, entonces 1 tiene dos hijos, el 4 y el 5 y su padre es el 0, en el mismo ejemplo los nodos verdes serían hojas. A los árboles en los que cada nodo tiene como mucho 2 hijos se les llama árbol binario.

Grafo generador: Grafo que resulta de extraer un cierto número de aristas (pueden ser 0) de un grafo.

Árbol generador: Grafo que resulta de extraer un cierto número de aristas (pueden ser 0) de un grafo, de modo que el grafo resultante sea un árbol.

Implementación

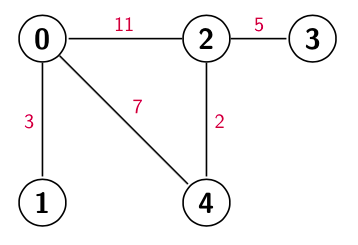
A continuación veremos las formas más habituales de representar un grafo. Para cada una de estas formas veremos la implementación de cómo leeríamos un grafo no dirigido y ponderado. Supongamos que el input del problema son dos enteros n y m, que representan el número de nodos (los cuales van de $0$ a $n-1$) y el número de arcos respectivamente. A continuación hay m líneas, cada una de ellas conteniendo 3 enteros: los nodos conectados por el arco, y su peso. Por ejemplo, el grafo de ejemplo que aparece en la explicación de grafo ponderado vendría dado como:

 

5 5
0 1 3
0 2 11
0 4 7
2 3 5
2 4 2

Los 3 modos más comunes de representar un grafo son:

• Como conjunto de arcos, donde guardamos las parejas de vértices conectados. En caso que el grafo sea ponderado se guardan tuplas: los dos nodos conectados y su peso.

#include <iostream>
#include <vector>

using namespace std;

int main() {
    int n, m;
    cin >> n >> m;

    vector <vector <int> > arcos(m, vector <int>(3));

    for (int i = 0; i < m; ++i){
        cin >> arcos[i][0] >> arcos[i][1] >> arcos[i][2];     
    }
}

• Como matriz de adyacencia, donde por cada par de vértices sabemos si hay un arco que los una o no. Si N es el tamaño del grafo, se guarda una tabla G[N][N] donde la entrada G[v][u] determina la información de la arista entre v y u. Habitualmente, G[v][u] valdrá 1 si existe un arco de v a u, y 0 en caso contrario. Sin embargo podemos modificarlo dependiendo del problema con el que trabajemos, por ejemplo, si queremos guardar un grafo con pesos positivos, la entrada G[i][j] valdrá el peso de la arista si existe, y -1 si no existe (podríamos usar cualquier otro número negativo o incluso asignarle un valor infinito según el problema).

#include <iostream>
#include <vector>

using namespace std;

int main() {
    int n, m;
    cin >> n >> m;

    vector <vector <int> > G(n, vector <int>(n, -1));

    for (int i = 0; i < m; ++i){
        int x, y, w;
        cin >> x >> y >> w;

        G[x][y] = G[y][x] = w;
    }
}

• Como lista de adyacencia. Guardaremos una lista G[N], donde cada entrada G[v] será una lista de los nodos adyacentes a v. En C++, podemos representarlo como vector<vector<int> > G. En caso de tener pesos, habrá que guardar también el peso de la arista, usando por ejemplo pair<int, int>. Otra opción sería tener un vector <vector <int> > W auxiliar de modo que si G[v][i] = u entonces W[v][i] es el peso del arco que va de v a u.

#include <iostream>
#include <vector>

using namespace std;

int main() {
    int n, m;
    cin >> n >> m;

    vector <vector <int> > G(n);
    vector <vector <int> > W(n);

    for (int i = 0; i < m; ++i){
        int x, y, w;
        cin >> x >> y >> w;

        G[x].push_back(y);
        G[y].push_back(x);
        W[x].push_back(w);
        W[y].push_back(w);
    }
}

Como norma general, acostumbra a ser más eficiente usar la última estructura.