Otro de los problemas clásicos de teoría de grafos es el de hallar el ancestro común más bajo (LCA por sus siglas en inglés) de dos nodos en un árbol. Recordamos que un árbol es un grafo conexo acíclico, y que dado un árbol podemos fijar un nodo como la raíz del cual cuelgan los demás nodos (para más información consulta el artículo sobre vocabulario de teoría de grafos). Dado un nodo en el árbol, todos los nodos que se hallan en el camino entre dicho nodo y la raíz son los ancestros del nodo. En este contexto, dados dos nodos en un árbol, queremos encontrar el nodo más lejano de la raíz que es ancestro de ambos nodos. Por ejemplo, en el siguiente árbol arraigado en el nodo 1:
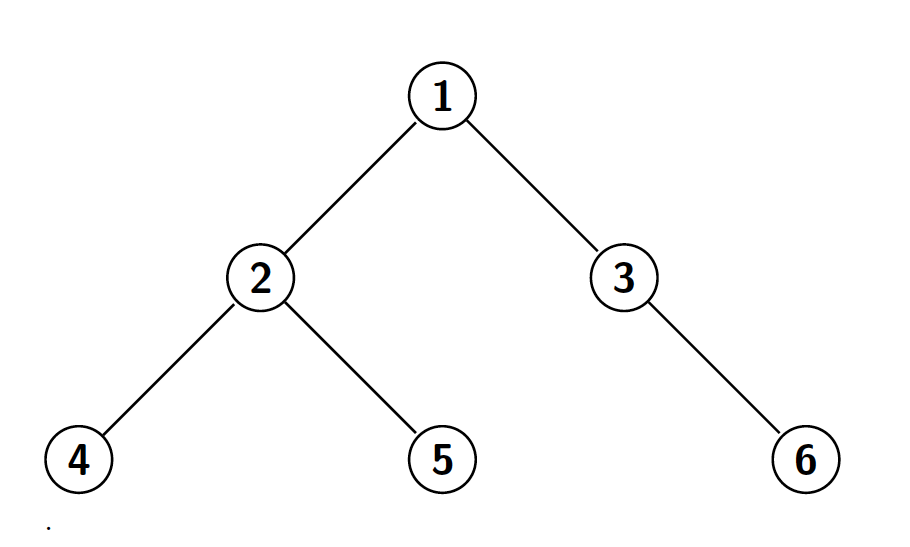
Los ancestros del nodo 5 serían los nodos 5, 2, y 1 (consideramos al propio nodo como uno de sus ancestros). Por poner algún ejemplo de LCA, el ancestro común más bajo de los nodos 4 y 5 sería el nodo 2, el de los nodos 5 y 6 sería el nodo 1 y el de los nodos 4 y 2 sería el 2. Veamos como podemos hallar dicho nodo eficientemente:
Binary Lifting
El primer algoritmo que vamos a ver consiste en guardar una representación del árbol que nos permita encontrar el LCA de dos nodos en $\mathcal{O}(\log{n})$. Para ello definimos $P_{v,i}$ como el ancestro a distancia $2^i$ del nodo $v$ (o la raíz si no tenemos ancestros a distancia $2^i$). En el ejemplo anterior, $P_{5,0} = 2$ y $P_{5,1} = 1$ ya que son los ancestros a distancia $2^0 = 1$ y $2^1 = 2$ del nodo 5. Además, definimos como $\text{entrada}_v$ y $\text{salida}_v$ el número de iteraciones (el tiempo o $t$) en un DFS que pasan hasta entrar o salir, respectivamente, del nodo $v$. Por ejemplo, en el árbol anterior, al hacer un DFS desde el nodo raíz (1), obtendríamos el siguiente camino:
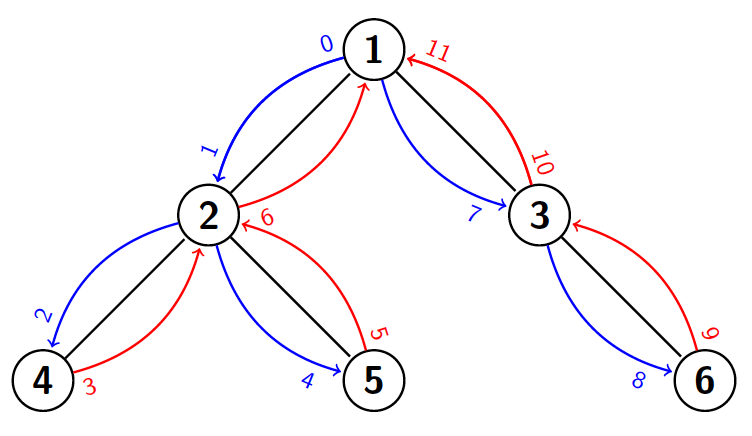
Empezamos desde el nodo 1, luego vamos al 2, después al 4, volvemos al 2, vamos al 5, ... Empezamos en la iteración $0$ (tiempo $= 0$) en el nodo raíz. A la siguiente iteración ($t = 1$) entramos en el nodo 2, y así sucesivamente. De este modo, cada nodo tiene asignado un tiempo de entrada y de salida. Por ejemplo, la primera vez que entramos en el nodo 2, es cuando $t=1$ y salimos por última vez cuando $t = 6$.
Una vez aclarada la nomenclatura veamos el algoritmo: Dado un árbol con $n$ nodos, calculamos $L = 1 + [log_2{n}]$ (donde [x] representa la parte entera de $x$). Luego, para cada nodo $v$ del árbol calculamos $P_{v,0}, P_{v,1}, \dots, P_{v, L}$ usando un DFS empezando desde la raíz (nótese que como $L = 1 + [log_2{n}]$, $P_{v, L}$ es siempre el nodo raíz, independientemente del nodo $v$). En particular, todos los ancestros de la raíz son la propia raíz y luego, por cada nodo $v$ que visitemos, como ya habremos calculado $P_{u,i}$ para todos los ancestros $u$ de $v$, podremos calcular $P_{v, i}$ como:
$P_{v, i} = \text{padre de v. si i = 0}$
$P_{v, i} = P_{P_{v, i-1}, i-1} \text{. si i > 0}$
Es decir, $P_{v, 0}$ es el padre de $v$ y $P_{v, i}$ es el ancestro a distancia $2^i$ de $v$ que es lo mismo que el ancestro a distancia $2^{i-1}$ del ancestro a distancia $2^{i-1}$ de $v$. Además, podemos aprovechar este mismo DFS para calcular, para todo nodo $v$, $\text{entrada}_v$ y $\text{salida}_v$. Nótese que un nodo $u$ es ancestro de un nodo $v$ si hemos visitado $v$ después de visitar $u$ y hemos salido de $v$ por última vez antes de salir de $u$ por última vez. O dicho de otro modo, $u$ es un ancestro de $v$ si y solo si $\text{entrada}_u < \text{entrada}_v$ y $\text{salida}_u > \text{salida}_v$.
Una vez hecho este comentario y tras haber calculado todo esto, podemos encontrar el LCA de dos nodos rápidamente de la siguiente manera:
Dados dos nodos $u, v$, queremos hallar el LCA de $u$ y $v$. Para ello, primero miramos si $u$ es ancestro de $v$ (en cuyo caso el LCA será $u$) o si $v$ es ancestro de $u$ (en cuyo caso $v$ será el LCA). Si ninguno de los nodos es ancestro del otro, miramos si $P_{u, L}$ es un ancestro de $v$. Si lo es, miramos si $P_{u, L-1}$ es un ancestro de $v$ y así sucesivamente hasta llegar a $P_{u, 0}$. Si en algún momento vemos que $P_{u, i}$ no es ancestro de $v$, entonces consideramos $u = P_{u, i}$ y seguimos el proceso mirando si $P_{u, i-1}$ es ancestro de $v$ (con la nueva $u$). Al final tendremos que $P_{u, 0}$ es el LCA de $u$ y $v$.
Veamos porque eso es así. Si de entrada $u$ es ancestro de $v$ o $v$ es ancestro de $u$, ya tenemos el LCA (es $u$ y $v$ respectivamente). Así que supongamos que el LCA de $u$ y $v$ es otro nodo $w$ distinto de $u$ y de $v$. Entonces, lo que estamos haciendo es considerando potencias de $2$ de mayor a pequeña hasta que encontremos una potencia ($2^i$) con la cual podamos subir esa distancia desde $u$ sin llegar a $w$. Cuando la encontremos subimos esa distancia, acercándonos a $w$. Como por definición, desde $u$ con $2^{i+1}$ llegábamos o nos pasábamos de $w$, desde el ancestro a distancia $2^i$ de $u$, si subimos otra vez $2^i$ llegaremos o nos pasaremos de $w$, con lo que podemos empezar desde el nuevo nodo mirando la potencia $2^{i-1}$. Ahora repetimos el proceso desde el nuevo nodo, mirando potencias de mayor a menor empezando por $2^{i-1}$. Como podemos escribir cualquier número con potencias distintas de $2$, podremos subir desde nuestra $u$ original hacia el hijo de $w$ que es ancestro de $u$ usando este método. Por lo que tenemos garantizado que, si el LCA de $u$ y $v$ no es ni $u$ ni $v$, al seguir el algoritmo que hemos descrito, al final nuestro nuevo nodo $u$ tendrá como padre $w$, es decir, el LCA de $u$ y $v$.
Aquí podemos ver un ejemplo del algoritmo:
// En este código asumimos que la raíz es el nodo 0.
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
typedef long long int ll;
typedef pair <int, int> ii;
typedef vector <int> vi;
typedef vector <vi> vvi;
// L = log2(n) y cnt es un contador para las iteraciones del DFS.
int L, cnt;
// P[v][i] es el ancestro 2^i-ésimo del nodo v
vvi P;
// G es la lista de adyacencia del grafo (G[v] contiene los vecinos de v).
vvi G;
// Primera y última vez que visitamos cada nodo.
vi first, last;
// Hacemos un DFS desde v donde parent es el padre de v (el padre de la raíz
// es la propia raíz) para calcular P[w][i] para todo nodo w. Aprovechamos
// también para calcular la primera y última vez que visitamos cada nodo.
void dfs(int v, int parent){
// Esta es la primera vez que visitamos v. Anotamos el tiempo y
// añadimos 1 al contador del tiempo.
first[v] = cnt++;
// Nos guardamos quien es nuestro ancestro a distancia 1 (nuestro padre).
P[v][0] = parent;
// Calculamos P[v][.]:
for (int i = 1; i <= L; ++i){
// El ancestro a distancia 2^i es el ancestro a distancia 2^(i-1)
// de nuestro ancestro a distancia 2^(i-1).
P[v][i] = P[P[v][i-1]][i-1];
}
// Visitamos todos nuestros hijos:
for (int u : G[v]){
// Vamos a todos nuestros vecinos que no sean nuestro padre.
if (u != parent) dfs(u, v);
}
// Anotamos cuando dejamos de visitar v y añadimos 1 al contador.
last[v] = cnt++;
}
// Devuelve true si u es un ancestro de v
bool ancestor(int u, int v){
// u es ancestro de v si lo hemos visitado antes que v y lo hemos
// dejado de visitar tras haber dejado de visitar v.
return (first[u] <= first[v] and last[u] >= last[v]);
}
// Devuelve el LCA de u y v (se asume que P, first y last ya estan
// calculados), es decir, que hemos llamado a la function init() antes.
int LCA(int u, int v){
// Si u es ancestro de v el LCA es u.
if (ancestor(u, v)) return u;
// Si v es ancestro de u el LCA es v.
if (ancestor(v, u)) return v;
// Visitamos todas las potencias de 2 de mayor a menor empezando por 2^L
for (int i = L; i >= 0; --i){
// Si el ancestro 2^i de u no es ancestro de v, subimos esa cantidad
// de nodos y actualizamos u.
if (not ancestor(P[u][i], v)) u = P[u][i];
}
// Ahora u es el nodo más lejano de la u original que no es ancestro de v.
// Por tanto, su padre es el LCA.
return P[u][0];
}
// Al llamar a esta función, calculamos los valores de L, P, first, last y cnt.
void init(int n){
L = 1 + log2(n);
P = vvi(n, vi(L+1));
first = last = vi(n);
cnt = 0;
// Cambiar los siguientes dos valores por el nodo raíz si este no fuera el nodo 0.
dfs(0, 0);
}
Observaciones:
- Antes de poder calcular el LCA eficientemente hay que precalcular los valores de P, first y last (llamar a la función init() en el código anterior). Calcular esos valores tiene coste $\mathcal{O}(n\log_2{n})$. Una vez calculados, cada llamada a la función LCA tiene coste $\mathcal{O}(\log_2{n})$
ETT
Hay otra manera de calcular el LCA entre dos nodos usando árboles de segmentos, este algoritmo usa la representación de un árbol como euler tour (técnica del euler tour o ETT). Primero tenemos que definir euler tour: el euler tour de un árbol es la secuencia de nodos que vamos visitando al hacer un DFS. Por ejemplo, en el grafo que teníamos anteriormente:
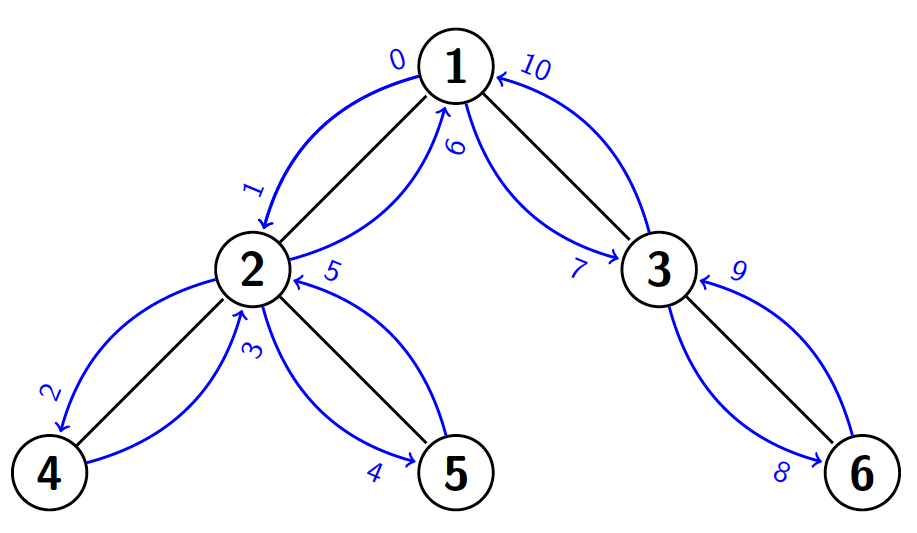
El euler tour estaría formado por los nodos: 1, 2, 4, 2, 5, 2, 1, 3, 6, 3, 1. Si nos fijamos en los nodos por los que pasamos entre la primera vez que visitamos un nodo $u$ y la última vez que visitamos un nodo $v$ (asumiendo que visitamos $u$ antes de $v$), se puede comprobar que el LCA de $u$ y $v$ es, de este conjunto, el que visitamos por primera vez antes. Esto es así porque, en primer lugar, sabemos que el LCA de dos nodos se encuentra en el camino que une a los dos nodos, por lo que al hacer un DFS y pasar de $u$ a $v$ tendremos que pasar por su LCA. En segundo lugar, como el LCA es ancestro de $u$ y $v$, al pasar por el LCA en el DFS, visitaremos $u$ y $v$ antes de volver al padre del LCA, con lo cual, no puede haber un nodo que hayamos visitado por primera vez antes que él.
Por lo tanto, para hallar el LCA de $u$ y $v$ (asumimos que $u$ lo hemos visitado antes que $v$ si no, giramos el argumento) simplemente miramos de entre los nodos que hemos visitado la última vez que hemos visitado $u$ y la primera vez que hemos visitado $v$, cuál es el nodo que hemos visitado por primera vez antes. En la siguiente tabla podemos ver del ejemplo anterior el euler tour y el order en que hemos visitado cada uno de los nodos por primera vez:
| Euler tour | 1 | 2 | 4 | 2 | 5 | 2 | 1 | 3 | 6 | 3 | 1 |
| Orden de la primera visita | 0 | 1 | 2 | 1 | 3 | 1 | 0 | 4 | 5 | 4 | 0 |
Por ejemplo, para calcular el LCA de 2 y 6, miramos del euler tour los nodos entre la última aparición del 2 y la primera del 6 (2, 1, 3, 6) y de ellos miramos cuál hemos visitado por primera visita antes (el 1 con pués es el primero que hemos visitado) y ese es el LCA. En la práctica, nos construimos la tabla anterior al hacer un DFS, junto con la primera y última aparición de cada nodo y, para calcular el LCA, buscamos el mínimo del intervalo de la segunda fila. En el ejemplo anterior, el mínimo elemento del segmento [5, 8] (es decir, 1, 0, 4, 5). Y la respuesta será el nodo que hemos visitado en ese momento. Para encontrar el mínimo de un intervalo rápidamente, hacemos servir un segment tree. Nota: en realidad podemos considerar el intervalo desde la primera vez que visitamos $u$ hasta la primera que visitamos $v$ o lo mismo pero con la última vez o cualquier variación (por ejemplo desde la primera vez que visitamos $u$ hasta la última que visitamos $v$).
A continuación podemos ver una posible implementación del algoritmo:
// En este código asumimos que la raíz es el nodo 0.
#include <iostream>
#include <vector>
using namespace std;
typedef vector <int> vi;
typedef vector <vi> vvi;
// G es la lista de adyacencia del grafo (G[v] contiene los vecinos de v).
vvi G;
// Orden en el que hemos visitado por primera vez los nodos del euler tour
// del grafo, empezando desde el 0. Es decir, si euler[7] = 3 es porque el
// octavo nodo del euler tour es el cuarto nodo que hemos visitado por
// primera vez.
vi euler;
// Tiempo en el que hemos visitado cada nodo (es decir, la posición de la
// primera aparición de cada nodo en el euler tour).
vi primera_visita;
// nodo_a_indice[v] representa el número de nodos que hemos visitado
// (por primera vez) antes que v. Es decir, si ordenamos los nodos por
// la primera vez que los hemos visitado v ocupa el lugar nodo_a_indice[v]-ésimo.
vi nodo_a_indice;
// Al revés de lo anterior: indice_a_nodo[i] representa el i-ésimo nodo que hemos
// visitado por primera vez (empezando por el índice 0).
vi indice_a_nodo;
// Contador del número de nodos que hemos visitado.
int cnt = 0;
// Número de hojas del segment tree. m es la menor potencia de 2 que es mayor
// o igual que el número de nodos del euler tour.
int m;
// Segment tree. Para i >= m, ST[i] = nodo_a_indice[euler[i-m]].
// Para 1 <= i < m ST[i] = min(ST[2*i], ST[2*i+1]).
vi ST;
// Representan la hoja de la izquierda y de la derecha del intervalo que cubre
// el nodo i-ésimo del ST. (L[1] = m, R[1] = 2*m-1).
vi L, R;
// Inicializa L y R recursivamente. Los argumentos son: un nodo del segment tree
// y la hoja de la izquierda y de la derecha del segmento que represente el nodo.
// Se tiene que llamar una vez con (1, m, 2*m-1).
void range(int p, int l, int r){
L[p] = l;
R[p] = r;
// Si es una hoja no bajamos más.
if (p >= m) return;
// Si no, actualizamos sus hijos.
range(2*p, l, (l+r)/2);
range(2*p + 1, 1 + (l+r)/2, r);
}
// Encuentra el mínimo del intervalo [l, r] que a su vez está cubierto por
// el intervalo que representa p. Si se llama con p = 1, entonces devuelve
// el mínimo valor del intervalo [l, r] a secas.
int findmin(int p, int l, int r){
if (l > R[p] or r < L[p]) return 1e9;
if (l <= L[p] and r >= R[p]) return ST[p];
return min(findmin(2*p, l, r), findmin(2*p+1, l, r));
}
// DFS para calcular el euler tour. Los argumentos son un nodo
// y su padre (o el propio nodo si v es la raíz del árbol).
void euler_tour(int v, int p){
// Índice que v ocupa en el euler tour.
primera_visita[v] = euler.size();
// Nos guardamos en que orden hemos visitado v.
nodo_a_indice[v] = cnt;
// Guardamos directamente en el euler tour el orden.
euler.push_back(cnt);
// Guardamos cual es el cnt-ésimo nodo que hemos visitado por primera
// vez y sumamos 1 al contador de nodos visitados.
indice_a_nodo[cnt++] = v;
// Miramos todos los hijos de v (vecinos que no sean nuestro padre).
for (int u : G[v]){
if (u == p) continue;
// Lo visitamos.
euler_tour(u, v);
// Y como volvemos a pasar por v añadimos el orden que ocupa otra
// vez en el euler tour.
euler.push_back(nodo_a_indice[v]);
}
}
// Calcula el LCA de v y u.
int LCA(int v, int u){
// Posición en qué v y u salen por primera vez en el euler tour.
int indice_v = primera_visita[v];
int indice_u = primera_visita[u];
// Si hemos visitado antes u cambiamos u y v. De modo que sabemos
// que v lo hemos visitado antes que u.
if (indice_v > indice_u) swap(indice_v, indice_u);
// Índice del mínimo número en euler desde indice_v hasta indice_u.
int min_index = findmin(1, m + indice_v, m + indice_u);
// Nodo al que corresponde dicho índice.
return indice_a_nodo[min_index];
}
// Inicializamos el segment tree y los vectores auxiliares.
void init(int n){
cnt = 0;
euler.clear();
primera_visita = indice_a_nodo = nodo_a_indice = vi(n, -1);
// Hacemos un DFS para calcular el euler tour. (Cambiar por euler_tour(
// raíz, raíz) si la raíz no es el nodo 0).
euler_tour(0, 0);
// calculamos m (la potencia más pequeña de 2 que es mayor o igual al número
// de nodos del euler tour).
m = 1;
while (m < euler.size()) m *= 2;
ST = L = R = vi(2*m, n);
// Inicializamos ST.
for (int i = 0; i < euler.size(); ++i) ST[m+i] = euler[i];
for (int i = m - 1; i >= 1; --i) ST[i] = min(ST[2*i], ST[2*i+1]);
// Inicializamos L y R.
range(1, m, 2*m-1);
}
Observaciones:
- Antes de poder calcular el LCA hay que calcular el euler tour y llenar el segment tree (llamar a la función init() en el código anterior). Calcular esos valores tiene coste $\mathcal{O}(n)$. Una vez calculados, cada llamada a la función LCA tiene coste $\mathcal{O}(\log_2{n})$
- Aunque el coste de inicializar las variables es menor en este algoritmo que en el de binary lifting, el coste de cada llamada a la función LCA es ligeramente mayor, ya que en este algoritmo la función es recursiva mientras que en el de binary lifting es iterativa. En general, es preferible usar binary lifting.
Aplicaciones
Este algoritmo suele ser útil cuando estamos tratando con caminos entre dos nodos en un árbol. Es útil en esos casos porque nos permite separar el camino de $u$ a $v$ en dos partes, un camino de $u$ a $LCA(u, v)$ y otro de $LCA(u, v)$ a $v$. Ambos caminos son de un nodo a un ancestro, eso nos permite calcular ciertas cosas fácilmente. Por ejemplo, si queremos contar el número de cosas que pasan entre $u$ y $v$, eso es el número de cosas que pasan de la raíz a $u$ + el número de cosas que pasan de la raíz a $v - 2 \cdot $ el número de cosas que pasan de la raíz a $LCA(u, v)$.
Un ejemplo clásico es contar la distancia entre $u$ y $v$. Si sabemos la distancia de cada nodo a la raíz, entonces $d(u, v) = d(u, \text{raíz}) + d(v, \text{raíz}) - 2 \cdot d(LCA(u, v), \text{raíz})$. Por lo tanto, al usar este truco, y tras inicializar todas las variables, podemos calcular la distancia entre dos nodos en un árbol en $\mathcal{O}(\log_2{n})$.


Añadir nuevo comentario