Una de las estructuras más importantes en algoritmia son los árboles binarios de búsqueda auto-balanceables; por poner un ejemplo, los sets y los maps de la librería estándar de c++ están implementados con este tipo de estructuras. Antes de ver este artículo es recomendable ver el de Tries, para estudiar un ejemplo más sencillo de una estructura que use punteros.
Tal y como dice el nombre, la estructura es un árbol binario, es decir, cada nodo tiene como mucho dos hijos. Además, es un árbol de búsqueda, esto significa que el valor de cada nodo es mayor que el de su hijo izquierdo y todos sus descendientes y, además, el valor de cada nodo es menor que el su hijo derecho y todos sus descendientes. A continuación se muestra un ejemplo de árbol binario de búsqueda:
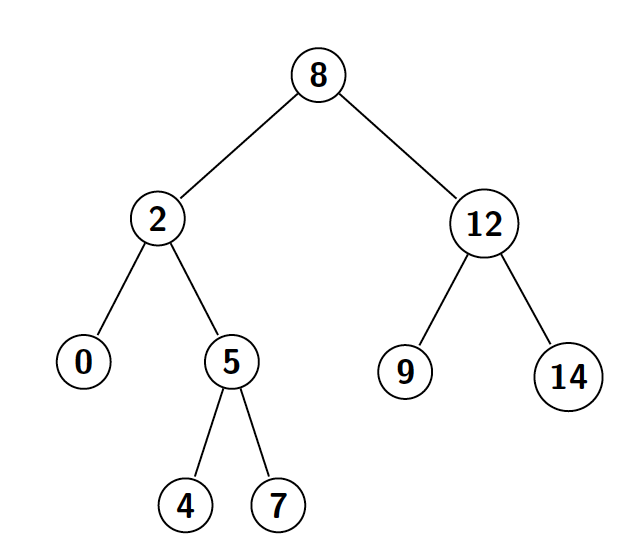
El hecho de que tenga esta propiedad (que sea de búsqueda), es muy importante, pues cuando buscamos un valor en el árbol, si empezamos por la raíz y vamos bajando, a cada paso podremos descartar uno de los lados del árbol. Por ejemplo, si buscamos donde se encuentra el número $9$ en el ejemplo anterior, empezaríamos por la raíz, y como $9 > 8$, sabemos que el número $9$ solo podrá estar en la parta derecha del árbol (pues todos los nodos a la izquierda del $8$ serán, por definición, menores que $8$). Esto nos permite encontrar números eficientemente (siempre y cuando el árbol tenga una estructura razonable), lo que da nombre a la propiedad.
Sin embargo, como ya hemos apuntado en el párrafo anterior, el hecho de que encontrar números sea eficiente, dependerá de la estructura del árbol. Por ejemplo, en el caso anterior, podríamos haber construido un árbol binario de búsqueda, donde la raíz fuese el $0$ y cada nodo solo tuviese un hijo a su derecha ($0, 2, 4, 5, 7, 8, 9, 12, 14$). Ese sería un árbol binario de búsqueda, pero hallar un número en concreto podría llegar a ser muy costoso. Por ejemplo, para saber si tenemos el número $14$, deberíamos atravesar todos los nodos. La estructura perfecta de árbol, aquella que, independientemente del nodo que buscásemos, tendría un menor coste de búsqueda, sería una donde cada nodo tuviese el mismo número de nodos a su izquierda que a su derecha. En ese caso, a cada nivel, podríamos descartar la mitad de los nodos, y como mucho tendríamos que visitar tantos nodos como la altura del árbol (que en este caso sería $\mathcal{O}\log_2(n)$, donde $n$ es el número de nodos). Un árbol binario cuya altura sea aproximadamente $\log_2(n)$ , se conoce como árbol binario balanceado .
Así pues, la estructura que nos interesa es un árbol binario de búsqueda que siempre esté balanceado, es decir, que al realizar cualquier operación sobre este (principalmente añadir o quitar un nodo), es árbol se balancee automáticamente. Es por eso que a estas estructuras se les llama árboles binarios de búsqueda auto-balanceables. Hay diversas maneras de implementar este tipo de árboles, algunos ejemplos de estructuras con esta propiedad son AVLs, Red-Black trees o Treaps. En este artículo explicaremos como implementar esta última estructura: los Treaps. Es una de las implementaciones más típicas de árboles binarios de búsqueda auto-balanceables en programación competitiva, por su relativa fácil implementación.
Treaps
Un Treap es un árbol binario donde cada nodo tiene dos valores, una prioridad, y su llave. La llave es el valor que realmente tiene el nodo, es el número que nos interesa y que caracteriza cada nodo. En cambio, la prioridad es un número auxiliar, cuyo objetivo es garantizar que el árbol resultante esté balanceado, de hecho, al crear un nodo, a este se le asigna una prioridad aleatoria. En particular, un Treap es un árbol de búsqueda respecto a su llave y es un max-heap respecto a su prioridad. Recordemos que, que un Treap sea un árbol de búsqueda respecto a su llave, significa que todos los nodos del subárbol que queda a la izquierda de un nodo, tienen una llave menor que el nodo en cuestión, mientras que todos los que queden a su derecha tendrán una llave mayor. Además, que un Treap sea un max-heap respecto a su prioridad, significa que cada nodo tiene una prioridad mayor que la de sus hijos. Que un Treap cumpla con estas dos propiedades nos garantiza que:
- Si no tenemos dos nodos con la misma llave o prioridad (y, normalmente, no los habrá), entonces dada una colección de nodos con una cierta llave o prioridad, existe un único Treap válido.
- Si las propiedades se asignan aleatoriamente, el árbol resultante estará balanceado con una muy alta probabilidad (básicamente con probabilidad $1$ para un número de nodos suficientemente grande).
En general, querremos hacer dos operaciones básicas sobre nuestro Treap: añadir nodos y quitar nodos. Veamos como realizar estas operaciones eficientemente:
Añadir nodos - split
La primera operación que vamos a ver es como añadir un nuevo nodo eficientemente. Para ello, antes vamos a establecer una cierta notación. En particular, dando un Treap $T$, denotaremos como $T \rightarrow l$ y $T \rightarrow r$ los Treaps que quedan a la izquierda y derecha de $T$ (es decir, aquellos que tienen como raíz el hijo izquierdo y derecho de la raíz original). Además, dado un nodo $v$, denotaremos $T(v)$ como el Treap que empieza en $v$.
Supongamos que tenemos un Treap $T$, y quereos añadir un nodo $v$ (con una cierta llave y prioridad, que asumiremos que son únicas, es decir, que no hay ningún nodo en el árbol que tenga la misma llave o prioridad). Lo que haremos será bajar por el árbol usando la propiedad de búsqueda respecto la llave hasta que, o bien lleguemos a una hoja, en cuyo caso simplemente añadiremos el nodo como hijo de la hoja, o hasta que encontremos un nodo con menor prioridad que $v$. Si al bajar encontramos un nodo $u$ con menor prioridad que $v$, entonces separaremos $T(u)$ en dos treaps $T(u)_1, T(u)_2$ de tal modo que todos los nodos de $T(u)_1$ tengan una llave menor a $v$ y todos los nodos de $T(u)_2$ tengan una llave mayor a $v$. Finalmente, substituiremos $T(u)$ por $T(v)$ donde $T(v) \rightarrow l = T(u)_1$ y $T(v) \rightarrow r = T(u)_2$.
Pero aún queda por ver un detalle: ¿Cómo separamos un Treap $T(u)$ en dos Treaps, de acuerdo con la llave de $v$? Lo haremos recursivamente. Dado un treap $T(a)$ con raíz $a$ (inicialmente $T(u)$ con raíz $u$), miramos si la llave de $a$ es mayor o menor a la de $v$. Si es mayor, separamos $T(a) \rightarrow l$ usando el mismo criterio en dos sub-treaps $(T(a) \rightarrow l)_1, (T(a) \rightarrow l)_2$ y, finalmente, $T(a)_1$ será $(T(a) \rightarrow l)_1$ y $T(a)_2$ será $T(a)$ substituyendo $T(a) \rightarrow l$ por $(T(a) \rightarrow l)_2$. Si, en cambio, la llave de $a$ fuese menor que la llave de $v$, entonces separaríamos $T(a) \rightarrow r$ en dos sub-treaps $(T(a) \rightarrow r)_1, (T(a) \rightarrow r)_2$ y, finalmente, $T(a)_2$ será $(T(a) \rightarrow r)_2$ y $T(a)_1$ será $T(a)$ substituyendo $T(a) \rightarrow r$ por $(T(a) \rightarrow r)_1$.
Al final, al usar este algoritmo conocido como split (separación), podremos añadir nodos en $\mathcal{O}(\log(n))$, ya que iremos desde la raíz a una de las hojas.
Quitar nodos - merge
Ahora vamos a ver cómo podemos quitar un nodo eficientemente. Para quitar un nodo $v$ con llave $k$, bajamos por el árbol usando la propiedad de orden, hasta encontrar el nodo con llave $k$, entonces unimos $T(v) \rightarrow l$ y $T(v) \rightarrow r$ en un solo Treap $X$ y substituimos $T(v)$ por $X$.
¿Pero como unimos los dos Treaps en uno? También usaremos recursión. Supongamos que tenemos dos Treaps $L(a), R(b)$ donde todos los nodos de $L(a)$ tienen una llave menor que cualquier nodo de $R(b)$. Si la prioridad de $a$ es mayor que la de $b$, entonces la solución $X$ será el Treap $L(a)$ substituyendo $L(a) \rightarrow r$ por la unión entre el Treap $L(a) \rightarrow r$ original con el Treap $R(b)$. Si en cambio, $b$ tiene mayor prioridad que $a$, la solución será $R(b)$ substituyendo $R(b) \rightarrow l$ por la unión del Treap $R(b) \rightarrow l$ original con $L(a)$.
Al usar este algoritmo, que se conoce como merge (unión), quitaremos un nodo en $\mathcal{O}(\log(n))$, pues iremos desde la raíz a dos hojas del árbol.
Implementación
A continuación mostramos una posible implementación de un Treap con sus operaciones habituales, más una operación adicional, busca, para ver si una llave ya se encuentra en el Treap. En este caso, definiremos un nodo del Treap como una estructura que contiene una prioridad y llave y que apunta a sus dos hijos. Además, usaremos el Treap como un set simplificado.
#include <iostream>
#include <random>
#include <chrono>
using namespace std;
typedef long long int ll;
typedef vector <int> vi;
typedef vector <vi> vvi;
std::mt19937 rng;
struct Node{
ll key, pr;
Node *l, *r;
};
typedef Node* Treap;
// Separamos el Treap T en dos Treaps L y R, de modo que todos
// los nodos de L tengan una llave menor a k y todos los nodos
// de R tengan un llave mayor a k.
void split(Treap T, ll k, Treap& L, Treap& R){
if (not T) L = R = nullptr;
else if (k < T -> key) {
split(T -> l, k, L, T -> l);
R = T;
}
else {
split(T -> r, k, T -> r, R);
L = T;
}
}
// Añadimos un nodo a al Treap T.
void insert(Treap& T, Treap a){
if (not T) T = a;
else if (a -> pr > T -> pr){
split(T, a -> key, a -> l, a -> r);
T = a;
}
else {
if (a -> key < T -> key)insert(T -> l, a);
else insert(T -> r, a);
}
}
// Juntamos los Treaps L y R en un único Treap T.
void merge(Treap& T, Treap L, Treap R) {
if (not L) T = R;
else if (not R) T = L;
else if (L -> pr > R -> pr) {
merge(L -> r, L -> r, R);
T = L;
}
else {
merge(R -> l, L, R -> l);
T = R;
}
}
// Quitamos un nodo com llave k (si existe) de T.
void erase(Treap& T, ll k) {
if (not T) return;
if (T -> key == k) merge(T, T -> l, T -> r);
else {
if (k < T -> key) erase(T -> l, k);
else erase(T -> r, k);
}
}
// Devuelve cierto si hay un nodo con llave k en el Treap T y falso si no.
bool find(Treap& T, ll k){
if (not T) return false;
if (T -> key == k) return true;
if (k < T -> key) return find(T -> l, k);
return find(T -> r, k);
}
// Insertamos un valor en el Treap solo si no existe previamente
void insert_value(Treap& T, ll k){
if (not find(T, k)){
Treap nodo_nuevo = new Node {k, rng(), nullptr, nullptr};
insert(T, nodo_nuevo);
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
// Inicializamos un generador de números aleatorios con el tiempo actual. Para que sea
// no que nunca tenga la misma seed.
rng = std::mt19937(std::chrono::steady_clock::now().time_since_epoch().count());
// Usaremos un Treap como set.
Treap my_set = nullptr;
// Añadimos el 1 y el 3
insert_value(my_set, 1);
insert_value(my_set, 3);
if (find(my_set, 1)) cout << "1 is in the set" << endl;
else cout << "1 is not in the set" << endl;
if (find(my_set, 2)) cout << "2 is in the set" << endl;
else cout << "2 is not in the set" << endl;
// borramos el 1 y el 2 (que no existe)
erase(my_set, 1);
erase(my_set, 2);
if (find(my_set, 1)) cout << "1 is in the set" << endl;
else cout << "1 is not in the set" << endl;
if (find(my_set, 3)) cout << "3 is in the set" << endl;
else cout << "3 is not in the set" << endl;
}
Notas y trucos
A continuación vamos a explicar un par de notas y trucos sobre como funcionan o como usar Treaps en determinados contextos:
- En un Treap, las operaciones para añadir o quitar nodos, así como para encontrar una llave, son todas $\mathcal{O}\log(n)$
- Para simplificar la explicación hemos asumido que las prioridades no se repiten, sin embargo, podemos considerar el caso de igualdad como cualquiera de los otros dos casos, de hecho, así está hecho en la implementación. Eso no es un problema porque, al tomar números aleatorios, no habrá muchos nodos con el mismo número. Si las prioridades tomasen valores en un rango pequeño, entonces esto sí que podría ser un problema.
- Si queremos poder tener nodos con la misma llave (tener un multiset en vez de un set), lo que se suele hacer es añadir una variable a los nodos, por ejemplo, int contador, que cuente cuantas veces aparece cada llave (por defecto los nodos tendrán contador $1$). Si queremos añadir un nodo que ya existe, añadimos $1$ al contador. Si queremos eliminar un nodo, lo eliminamos solo si su contador es $1$, si no, simplemente quitamos $1$ al contador.
- Siempre que generemos números aleatorios, y eso incluye a los Treaps, es muy recomendable usar los siguientes dos trucos:
- En primer lugar, usar std::mt19937, como en la implementación, en vez de la función rand(). Hay tres motivos para hacer esto:
- El generador es de mayor calidad, es decir, los números generados son "más aleatorios".
- Es más eficiente en producir un número aleatorio (es hasta $3$ veces más rápido).
- El más importante, rand tiene un rango bastante menor de números que puede generar, en particular, rand() genera números de $0$ a $32767$ mientras que mt19937 los genera de $0$ a $4294967295$.
- En segundo lugar, es recomendable usar como seed del generador el tiempo actual. Así garantizamos que la seed sea siempre distinta, independientemente del compilador, evitando que alguien sea capaz de construir un caso donde nuestro Treap deje de ser balanceado.
- En primer lugar, usar std::mt19937, como en la implementación, en vez de la función rand(). Hay tres motivos para hacer esto:
- En los nodos podemos tener más variables. Por ejemplo:
- Podemos añadir una variable value, lo que haría que pudiésemos usar un Treap como map.
- Otra de las variables típicas para añadir a un Treap es el número de nodos del sub-treap (o número de hijos). Utilizando esto podemos calcular índices; por ejemplo, cuál es la llave que ocuparía el puesto $24$ si las ordenásemos. En otras palabras, podemos tener un set indexado, donde podríamos calcular my_set[x] en $\mathcal{O}(\log(n))$. Es importante recordar que al añadir o quitar nodos, habría que actualizar ese valor. Por ejemplo, para actualizarlo podemos usar esto y hacer update(T), update(R) o update(L) donde toque:
-
int childs(Treap& T){ if (not T) return 0; return T -> childs; } void update(Treap& T){ if (not T) return; T -> childs = 1 + childs(T -> l) + childs(T -> r); }
- Finalmente, recordar que un Treap, al final, no deja de ser un árbol y, por tanto, podemos utilizar otros trucos que usamos en otras estructuras de datos que también sean árboles. Por ejemplo, con Treaps también podemos utilizar lazy propagation.


Añadir nuevo comentario