Graph traversal

Recorrer un grafo es, sin lugar a dudas, uno de los procesos más útiles al tratar con grafos. En esta sección veremos los dos métodos más frecuentes a la hora de recorrer un grafo, es decir, dado un nodo visitar todos los vértices conectados a él.

DFS

El algoritmo más sencillo es el llamado DFS (depth first search o búsqueda en profundidad). La idea del algoritmo es, empezando por el nodo original, visitar cada uno de sus vecinos no visitados, al visitar uno de estos vecinos (v) visitamos todos los vecinos no visitados de v y vamos repitiendo este proceso hasta que no queden nodos no visitados conectados al original. Nótese que al encontrar un vecino lo visitamos antes siquiera de acabar de ver cuales eran nuestros demás vecinos.  Veamos un ejemplo:

Vamos a recorrer el grafo dado, desde el nodo 0, el procedimiento sigue:

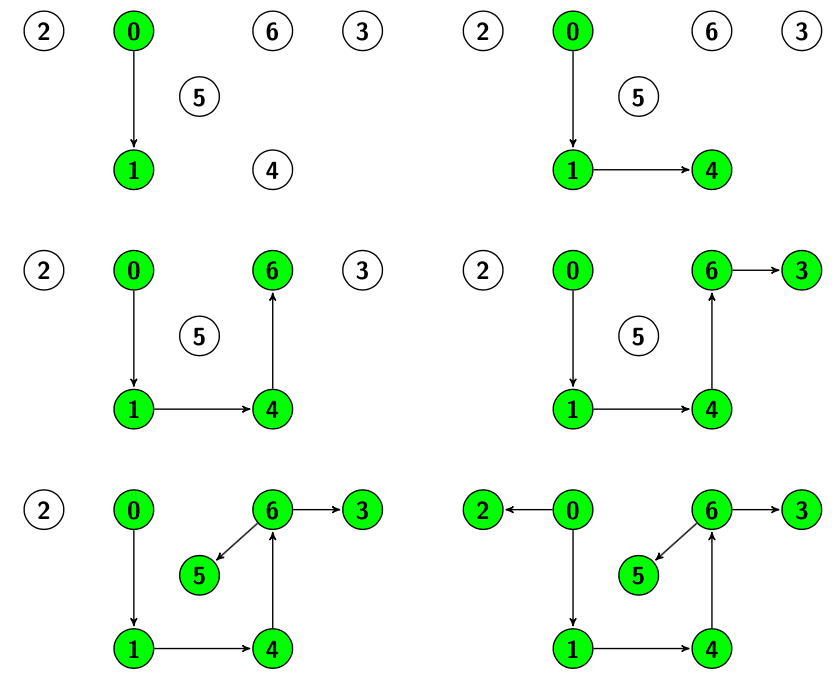
En el ejemplo podemos ver cómo no visitamos el segundo vecino de 0, (el nodo 2), hasta que no hemos acabado de visitar completamente el primer vecino (el nodo 1). Nótese también que algunos de nuestros vecinos los habremos visitado mediante vecinos de nuestros vecinos.

Observaciones:

• Al realizar el algoritmo de DFS se obtiene un árbol.
• El algoritmo es también aplicable a grafos dirigidos.
• La complejidad del algoritmo es $\mathcal{O}(|E|+|V| )$

La idea fundamental que hay detrás de la implementación del algoritmo es tener un vector de booleanos que dado un nodo nos diga si ha sido visitado y, crear una función recursiva que dado un nodo, si no ha sido previamente visitado, visite a todos sus vecinos.
 

vector <bool> visited (n, false); // visited[v] es cierto sii hemos visitado v
vector <vector <int> > G; //grafo G[v] es un vector con los vecinos de v

// dado un nodo v visita a todos los nodos conectados a v
void dfs (int v) {
    if (visited[v]) return;
    visited[v] = true;

    for (int i = 0; i < G[v].size(); ++i){ //iteramos por todos los vecinos
        int u = G[v][i];
        dfs(u); //lo visitamos
    }
}

Es decir, la idea clave es que cuando queremos visitar un nodo, visitamos recursivamente antes todos sus vecinos que no han sido visitados (que habrán explorado a su vez antes de devolver la llamada).

BFS

El otro algoritmo fundamental a la hora de recorrer un grafo es el  llamado BFS (breadth first search o búsqueda en anchura) sirve normalmente para encontrar distancias en un grafo sin pesos (aunque recorrer los nodos en anchura puede tener otras aplicaciones).  En este caso, se visitan los nodos ordenados por la distancia al origen, es decir, visitamos todos los nodos a distancia 1 del original, luego los de distancia 2… La idea del algoritmo es ir añadiendo en una lista, qué nodos hay que visitar. Vistamos el nodo original, cada uno de sus vecinos no visitados serán apuntados en la lista, manteniendo el orden de la misma, al acabar, iremos al primer nodo de la lista y si no lo hemos visitado repetiremos el procedimiento, luego iremos al segundo nodo de la lista y si no lo hemos visitado repetiremos el procedimiento...  y así hasta que completemos la lista. Veamos como se aplicaría este algoritmo en el ejemplo anterior:

Empezando de nuevo desde el nodo 0, recorremos el grafo:
 

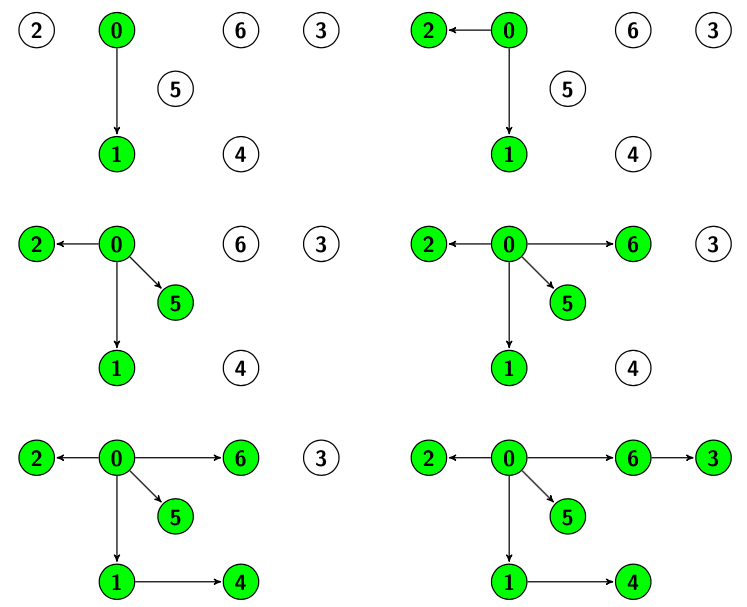
Observaciones:

• Al realizar el algoritmo de BFS también se obtiene un árbol.
• El algoritmo es también aplicable a grafos dirigidos.
• La complejidad del algoritmo es $\mathcal{O}(|E|+|V| )$

Para llevar a cabo la implementación del algoritmo tendremos un vector de booleanos que nos diga si hemos visitado un nodo, y una cola que representará nuestra lista de nodos a visitar. He aquí un ejemplo:

vector <bool> visited;
vector <vector <int> > G;

void bfs(int v){
    queue <int> Q; //u otra estructura que sirva de cola
    Q.push(v); //empezamos con el nodo origen

    while (not Q.empty()){ //mientras nuestra lista tenga nodos
        int u = Q.front(); //seleccionamos el primer nodo de la lista
        Q.pop(); //y lo eliminamos

        if (not visited[u]){ //si no lo hemos visitado
            visited[u] = true;

            for (int i = 0; i < G[u].size(); ++i){
                int w = G[u][i];

                Q.push(w); //ponemos a sus vecinos en la lista
            }
        }
    }
}

Como añadimos los vecinos al final de la cola, aseguramos que se preserva el orden deseado. Si queremos mantener la distancia, podemos pasar una pareja de enteros en la cola o guardar directamente la distancia con una pequeña modificación del pseudocódigo (véanse las soluciones de los problemas).

Algoritmos que usan DFS o BFS:

• Mínima distancia entre nodos en grafos no ponderados
• Ordenación topologica
• Componentes fuertemente conexas
• 2 - SAT
• Puntos de articulación/puentes
• LCA
• Maxflow/mincut
• etc