Prerrequisitos
Para entender este manual, es necesario conocer bien las técnicas principales de exploración de grafos, como BFS y DFS. Además, muchos problemas sobre HLD lo combinan con árboles de segmentos, por lo que es bueno conocerlos también.
Aunque no es necesario y hay varias implementaciones que no lo usan, creo que la implementación más intuitiva de HLD es la que usa binary lifting y LCA, por lo que conviene conocer estos conceptos antes de seguir con el manual.
Introducción
Heavy-Light Decomposition (comúnmente abreviado como HLD) es un algoritmo que descompone árboles, cuyos nodos contienen algún valor (es decir, tenemos una función $v$ que, dada el índice $x$ de un nodo, $v(x)$ es un número de nuestro interés), de forma que nos sea fácil responder consultas del tipo:
- Para dos nodos $x$ e $y$ del árbol, actualiza $v(w)$ para todos los nodos $w$ en el camino entre $x$ e $y$.
- Dados dos nodos $x$ y $y$ del árbol, encuentra el máximo valor, el mínimo valor o la suma de los valores de los nodos en el camino entre $x$ e $y$. Más concretamente, dada una función $f$ que toma una lista de números y retorna un único valor, podemos calcular $f((v(w_0 = x), v(w_1), \dots, v(w_k = y)))$, siendo $w_0, \dots, w_k$ los nodos en el camino entre $x$ e $y$. $f$ además ha de tener la propiedad de que $f((a, b, c)) = f(a, f(b, c))$.
Ten en cuenta que aquí usamos camino entre $x$ y $y$ en singular ya que, al ser un árbol, una de las características del grafo es que para toda pareja de nodos $x$ e $y$ en este, hay exactamente un camino que la conecta.
La mayoría de problemas de HLD consisten en descomponer el árbol en caminos (en breve veremos exactamente cómo) y, sobre cada camino, construir un árbol de segmentos o árbol de Fenwick, sobre el que más adelante operaremos.
Definiciones
El algoritmo HLD (como su propio nombre indica) basa su funcionamiento en la división de las aristas, caminos e hijos ligeros y pesados. Escogeremos un nodo arbitrariamente como raíz del árbol (normalmente el que tiene índice 0 por simplificar). Llamaremos entonces hijos de la raíz a los nodos que, si iniciáramos una DFS desde la raíz, exploraríamos a través de una arista directa desde la raíz y así sucesivamente con todos los nodos $u$, siendo sus hijos los explorados en esta DFS desde la raíz a través de una arista directa desde $u$ al nodo.
Para cada nodo $u$, partiremos sus hijos en pesados y ligeros. Más concretamente, el hijo cuyo subárbol tenga mayor tamaño (escogeremos arbitrariamente en caso de empate) será el denominado hijo pesado y, en caso de haber más hijos, el resto serían ligeros. Por lo tanto, si un nodo $u$ tiene $n \geq 1$ hijos, siempre tendrá un único hijo pesado y $n-1$ hijos ligeros. Las aristas que conecten a un padre con un hijo pesado serán aristas pesadas, mientras que las aristas que conecten a un padre con un hijo ligero serán aristas ligeras. Dado que el grafo es un árbol, toda arista caerá en exactamente una de estas dos categorías. Finalmente, diremos que un camino por el árbol es un camino pesado si todas sus aristas son pesadas, mientras que si son todas ligeras, diremos que es un camino ligero. Podemos observar que no todos los caminos han de ser o pesados o ligeros, ya que un camino puede combinar aristas de ambos tipos.
Funcionamiento del algoritmo
Paso 1: Escogemos una raíz arbitraria, normalmente el nodo con índice 0.
Paso 2: Iniciamos una DFS desde la raíz para calcular el tamaño del subárbol bajo cada nodo, incluyéndolo a sí mismo. Además, para cada nodo iremos guardando cuál es su hijo pesado, si es que tiene hijos. En caso de empate, escogeremos un hijo arbitrariamente. Podemos ver el siguiente ejemplo, donde las aristas que conectan a cada nodo "padre" con su hijo pesado están coloreadas de verde.
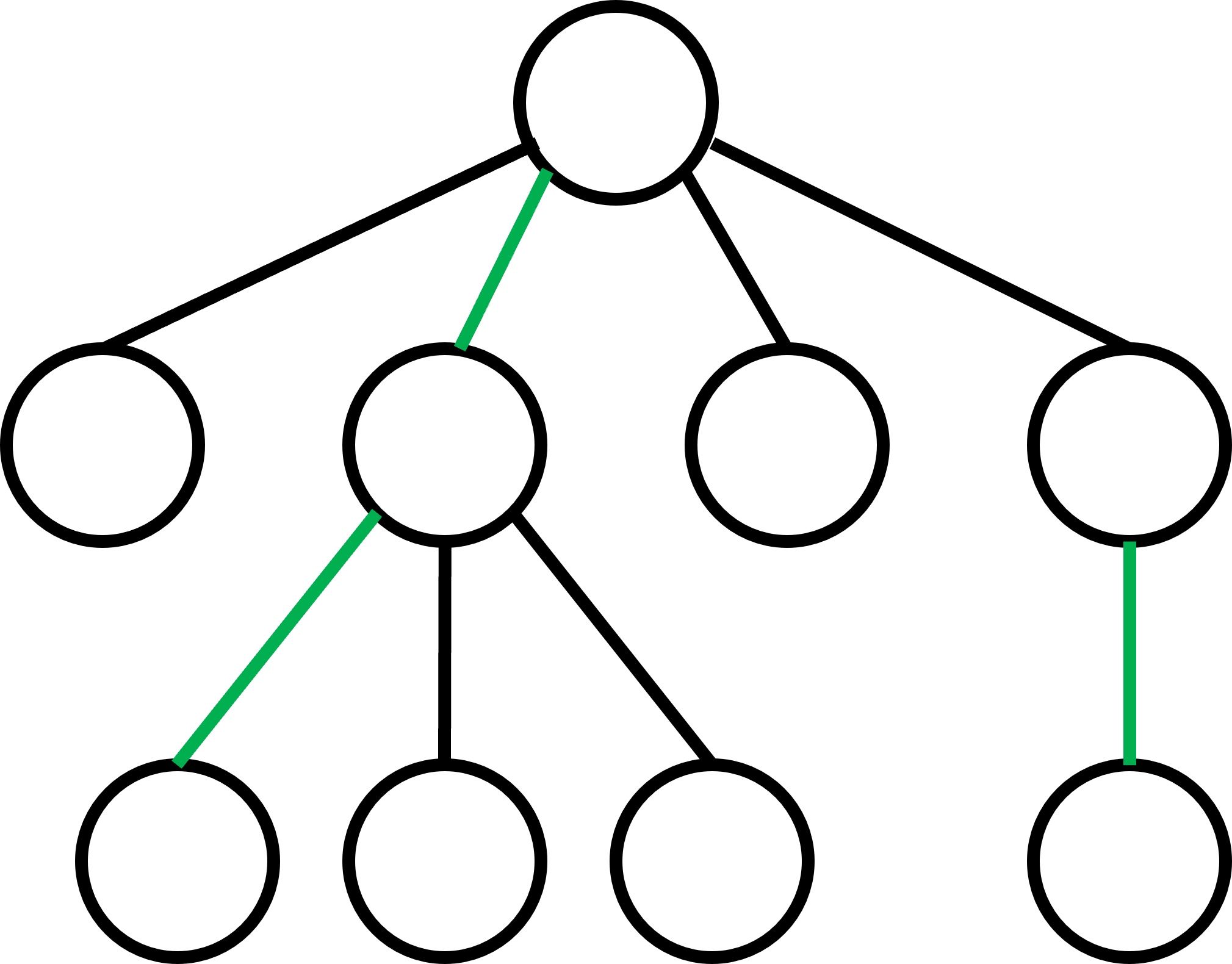
La clave del funcionamiento de este algoritmo es que cualquier camino por el árbol pasará por, como mucho $\log(n)$ aristas ligeras (negras en el diagram anterior), siendo $n$ el número total de nodos en el árbol. Esta no es una observación trivial y, aunque no la demostraremos en este manual, podéis leer la demostración si os interesa aquí. Además, como consecuencia, cada camino pasará por, como mucho, $\log(n)$ caminos pesados.
Por último, dados dos nodos $x$ e $y$, podemos partir el camino entre los dos nodos en dos: el camino de $x$ a LCA($x$, $y$) y el camino de LCA($x$, $y$) a $y$. Si necesitamos que los caminos no se solapen, podemos simplemente coger el de $x$ al hijo de LCA($x$, $y$) que sea ancestro de $x$, por ejemplo. Asumiremos entonces de ahora en adelante que toda consulta (ya sea de cambio de valores o de cálculo de una función sobre estos) será sobre un camino entre un ancestro y un nodo que desciende de este.
Paso 3: podemos, para cada camino pesado, construir un árbol de segmentos o de Fenwick que calcule $f$ sobre un rango del camino, ordenando los valores de los nodos en función de en qué posición aparecen en el camino.
Paso 4: dados dos nodos $a$ y $b$, siendo $a$ ancestro de $b$, podemos calcular $f$ sobre el camino de $a$ a $b$ calculando primero $f$ sobre los rangos de caminos pesados que se encuentran entre $a$ y $b$ (usando el árbol de segmentos/Fenwick de cada camino) y luego calculando $f$ de estos valores y los de las aristas ligeras, obteniendo el resultado que buscamos. Operamos de la misma forma si lo que buscamos es cambiar los valores de los nodos entre $a$ y $b$.
Complejidad
Preprocesado: la complejidad de la DFS es $O(n)$. Lo mismo (o algo más: $O(n \log n)$ si se usa segtree o se construye el BIT de forma naïve) la de construir los árboles de segmentos/Fenwick por camino. Por lo tanto, la complejidad del preprocesado es de $O(n) + O(n) = O(n)$ (o de $O(n \log n)$ en el caso explicado antes).
Cambiar/calcular $f$ sobre los valores en el camino entre dos nodos: este camino estará formado por $O(\log n)$ aristas ligeras y $O(\log n)$ caminos pesados. Cambiar/mirar el árbol de segmentos de cada camino nos llevará $O(\log n)$, por lo que la complejidad total será $O(\log n + \log^2 n) = O(\log^2 n)$.
Ejemplo
Un problema que nos será útil para implementar HLD (y comprobar la corrección de nuestra implementación) es CSES- Path Queries. Trata de implementar tú la solución con las instrucciones de este manual antes de ver la solución:
#include <iostream>
#include <vector>
using namespace std;
int N, Q;
vector<vector<int>> adjList, HLD;
vector<int> val, profundidad, subT, par;
vector<pair<int, int>> posicionCaminos; // posicionCaminos[nodo] = (índice del camino pesado al que pertecene, índice en el camino en el que se encuentra)
vector<vector<long long int>> BIT;
// Hacemos una DFS donde para cada nodo nos guardamos su profundidad, padre y tamaño del subárbol
void dfs(int S, int p) {
int ans = 0;
for (int v: adjList[S]) {
if (v == p) continue;
profundidad[v] = profundidad[S]+1;
par[v] = S;
dfs(v, S);
ans += subT[v];
}
subT[S] = ans+1;
}
// Descomponemos el árbol en caminos pesados
void decompose(int node, int chain) {
HLD[chain].push_back(node);
posicionCaminos[node] = make_pair(chain, (int) HLD[chain].size()-1);
// encontramos el hijo pesado del nodo
int sz = -1, ch = -1;
for (int v: adjList[node]) {
if (profundidad[v] < profundidad[node]) continue;
if (subT[v] > sz) {
sz = subT[v];
ch = v;
}
}
if (sz == -1) return; // no tiene hijo pesado -> retornamos
decompose(ch, chain); // descomponemos el subárbol del hijo pesado
for (int v: adjList[node]) {
// descomponemos el subárbol del resto de hijos
if (profundidad[v] < profundidad[node] || v == ch) continue;
HLD.push_back(vector<int>());
decompose(v, HLD.size()-1);
}
}
// las siguientes dos funciones son de cambios y consultas en BITs (nada nuevo de este manual)
void add(int ch, int pos, long long int num) {
while(pos < (int) BIT[ch].size()) {
BIT[ch][pos] += num;
pos = pos | (pos+1);
}
}
long long int encontrarSumaCamino(int ch, int pos) {
long long int ret = 0ll;
pair<int, int> curP;
int p;
while(ch >= 0) {
while(pos >= 0) {
ret += BIT[ch][pos];
pos = (pos & (pos+1))-1;
}
p = par[HLD[ch][0]];
if (p == -1) break;
curP = posicionCaminos[p];
ch = curP.first;
pos = curP.second;
}
return ret;
}
// construimos el grafo sobre el que trabajaremos
void construirGrafo() {
adjList.assign(N, vector<int>());
profundidad = vector<int>(N);
profundidad[0] = 0;
val = vector<int>(N);
subT = vector<int>(N);
par = vector<int>(N);
par[0] = -1;
for (int i = 0; i < N; i++) cin >> val[i];
int a, b;
for (int i = 0; i < N-1; i++) {
cin >> a >> b;
adjList[a-1].push_back(b-1);
adjList[b-1].push_back(a-1);
}
}
// encontramos los caminos pesados del grafo
void partirEnCaminos() {
dfs(0, -1);
posicionCaminos.assign(N, pair<int, int>());
HLD = vector<vector<int>>(1, vector<int>());
decompose(0, 0);
}
// creamos un BIT por camino pesado
void construirBITs() {
for (int i = 0; i < (int) HLD.size(); i++) {
BIT.push_back(vector<long long int>(HLD[i].size(), 0));
for (int j = 0; j < (int) HLD[i].size(); j++) {
add(i, j, val[HLD[i][j]]);
}
}
}
// recogemos y procesamos los dos tipos de consulta
void procesarConsulta() {
int a, c;
long long int num;
cin >> c;
if (c == 2) {
cin >> a;
a--;
cout << encontrarSumaCamino(posicionCaminos[a].first, posicionCaminos[a].second) << "\n";
} else {
cin >> a >> num;
a--;
add(posicionCaminos[a].first, posicionCaminos[a].second, num - val[a]);
val[a] = num;
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
cin >> N >> Q;
construirGrafo();
partirEnCaminos();
construirBITs();
while(Q--) {
procesarConsulta();
}
return 0;
}


Añadir nuevo comentario